如果生物学就像数学，我们的命运将是预先确定的：每一个细胞分裂、有机体、个体和种群都会在逻辑上遵循基本真理或公理。令人高兴的是，生物学并不完全遵循模式和秩序的科学——突变、变异和随机机会导致了一个丰富多样的生物学研究领域。
话虽如此，数学确实渗透到生活世界中。从著名的鹦鹉螺壳的对数曲线到捕食者和猎物种群的回声周期性，几乎在每个生物过程中都可以找到数学的证据。但从历史上看，这两个领域沿着不同的路径发展。数学由从公理得出的陈述组成，数学研究的应用通常在几十年甚至几个世纪之后。生物学开始并继续关注可观察的现象，没有相应的生物学公理或“第一原理”。
但近年来，这一差距开始缩小。数学生物学——或者说数学在生物学中的应用——已经成为它自己的跨学科领域，对生物学和数学的“纯”领域都有影响。
“在过去的几十年里，发生了一场复兴并重新定义了数学生物学家的意义：是简单地应用现有的数学工具并对其进行调整以获得生物学见解，还是提出新的数学问题，这些问题和观点启发了数学生物学家。生物学？” Nina Fefferman 说，国家数学和生物合成研究所所长。 “这两种实践现在密不可分地交织在一起，以便在开发新数学的地方获得这种美妙的反馈，因为它有助于扩展我们对生物学的理解，这也表明我们可以如何以新的方式重新思考数学本身。 ”
为了促进这一新兴跨学科领域的合作和研究，美国国家科学基金会于 2017 年与西蒙斯基金会合作创建了四个NSF-西蒙斯复杂生物系统数学中心。成立以搜索 NSF 所谓的“生活规则” ，总部设在哈佛大学；西北大学；加州大学欧文分校；和佐治亚理工学院，这些中心允许跨学科的科学家在定量生物学的前沿进行创新。
“如果我们正确地提出问题，就有一个围绕基本生物学问题发明新数学框架的绝佳机会，”哈佛大学 NSF-西蒙斯中心研究执行主任布里奇特奎南说。
生活是什么？活细胞的物理方面于 1944 年首次出版。图片来源： Wikimedia Commons-OG.JPG){kind=link}
超越还原论
尽管自 19 世纪初以来生物学家一直在使用数学工具（例如，数学图表出现在 Gregor Mendel 的开创性论文“植物杂交实验”和查尔斯达尔文的开创性著作《物种起源》中） ，但它已经采取了几十年甚至几百年的时间，研究人员开发基于生物学事实的数学工具，而不是从物理学和非生命系统中借来的工具。
二战前后，专注于为生命提供动力的生化实体的分子生物学开始兴起。 1944 年，数学物理学家 Erwin Schrödinger 写了一本短书，名为《展示物理和化学如何帮助解决生物学问题》。生物学家詹姆斯沃森和物理学家弗朗西斯克里克都认为生命是什么？启发他们寻找双螺旋结构和诱人的 DNA 代码（由 Rosalind Franklin 用 X 射线晶体学发现）。在那之后，来自众多学科的科学家开始涌向分子生物学。
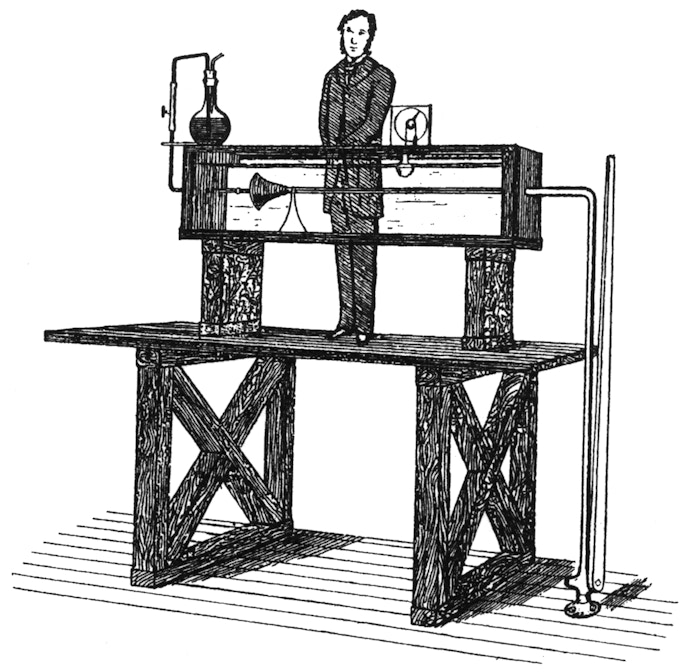插图取自流体动力学家 Osborne Reynolds 在 1883 年发表的有影响力的论文“关于确定平行通道中水的运动是直接还是弯曲的环境以及平行通道中的阻力定律的实验研究”。水从实验者附近的水箱通过透明管流到地下；染料在流动的中间注入。因此可以精确地观察到流动的湍流或层流性质。学分：维基共享资源
物理学家带来了还原论的哲学框架，即剔除所有“外部”因素而只关注问题的一部分的做法。在一个著名的 1883 年例子中，突出了物理学几个世纪的还原论，流体力学先驱奥斯本雷诺兹研究了玻璃管内的水流，而不是海浪中的水流。正如西北大学 NSF-西蒙斯定量生物学中心主任理查德·卡修所说，还原论“从根本上彻底改变了我们许多人研究生物学的方式。”
今天，许多生物学研究仍然坚定地在还原论范式中运作。 “许多人相信分子将成为生物学的答案，”奎南说。 “人们非常相信我们可以‘暴力破解’重要的问题——如果我们以原子分辨率测量每一个分子、每一个突触、每一个细胞相互作用，如果我们只是获得更多数据，那么，不知何故，知识就会出现。当然，拥有数据很棒，拥有计算能力也很棒。但再多的审问也不会迫使分子披露他们没有的信息。”
因此，对生物学的深刻理解可能不会来自于将事物切割成越来越小的碎片，并期望信息能够像物理学从还原论中表现出来的方式一样。这是因为物理学处理的是非生物，而生物学处理的是生命的复杂性。 1960 年，物理学家尤金·维格纳 (Eugene Wigner) 发表了《自然科学中数学的不合理有效性》一文，论述了我们可以进行观察、记下方程、操纵它们并在现实中做出实际预测是多么“不合理”。世界。但是我们在物理学中一直使用这样的数学。然而，维格纳还预测，找到相应的生命方程将“更加困难和混乱”。
“物理学家通过关注相对简单的问题并剔除外部因素，成功地使用了还原论框架，”Queenan 说。 “根据定义，生物的行为并不那么简单，如果我们去掉外部因素，生物就会死亡——此时我们可以成功地使用物理学方程来预测它们的行为。”
“你没有意识到的是，数学和物理界需要什么才能达到可以将自然问题浓缩为特定积分计算的水平，”西北数学家马达夫·马尼 (Madhav Mani) 说。他认为生物学需要超越还原论来寻找这些方程的下一步，尽管这因该领域的独特因素而变得复杂。 “在生物学中，大多数时候，由于其相对的理论和概念处于起步阶段，忘记了积分，你甚至不确定变量应该是什么。我相信在我们对生命和生物物质的研究中，我们会遇到变量错误的问题。”
Mani 以流体动力学、代数几何和其他著名的复杂领域为例，观察到“当我们刚刚找到正确的变量时，它们就很简单。”
正面迎接生物学的挑战
多年来，数学在物理学中的应用非常丰富。维格纳的“数学在科学中的不合理效力”就是证明。但生物学要复杂得多：每个个体有机体都会适应一系列因素，从基因组的构成到生态系统的复杂性。除了适应这些因素外，生命系统还具有许多相互关联的部分和“涌现”的特性：其表现超出单个部分的能力的特征。例如，在大脑中，一个神经元的单个轴突只会发送有限的电脉冲，但结合数亿个这些脉冲会产生像记忆一样复杂的东西。
西北中心的计算生物学家 Rosemary Braun 指出：“生命系统只是具有所有这些美丽且非常有趣的复杂性，而物理理论无法很好地处理这些复杂性。”
物理学并没有提供一种直接的方法来衡量一个物种中个体之间的差异。这就是数学生物学可以介入的地方，正如最近由西北大学的一个团队领导的对果蝇的研究中所看到的那样。由于不同种类的果蝇适应不同环境的方式，果蝇的翅膀在微小但重要的方面有所不同。在西北大学，生物学家 Carthew 与数学家 Mani 合作找出了衡量差异的度量标准或严格的方法。较旧的指标识别视觉“地标”，例如特定的静脉交叉点，并测量这些地标之间的距离以创建粗略的指标：地标指标中的“更近”的翅膀在其地标之间具有相似的距离。但是人类任意选择的地标并不能封装所有关于翅膀的数据。
相比之下，西北大学团队采用的方法保留了更多关于机翼特征的信息，例如静脉之间的角度、机翼内的毛发和边缘刷毛。 Carthew 的实验室煞费苦心地拍摄了数千张果蝇翅膀的照片； Mani 将图像几何映射为统一格式。使用一种称为光谱分解的工具，他们发现了一个单一的数学“模式”，所有单独的机翼都沿着该模式不同。这意味着当果蝇以不同的基因组序列、温度或饮食饲养时，它们会沿着这种数学模式而有所不同。值得注意的是，这个新指标还检测到进化差异：物种分化时间越长，翅膀在数学模式上的距离就越远。
尽管 Mani 使用的数学工具已经存在了几十年（有些甚至几个世纪），但真正的创新在于提出问题并找出应用哪种数学。
“事实是，以前没有人这样做过，”Mani 说。 “我们经历了四年的过程：确定问题、寻找解决问题的方法、找到数学部分、开发工具，最后进行实验。”
数学生物学充满了像 Carthew-Mani 合作这样的例子，这两个领域的人都可以实现他们自己都无法实现的飞跃。正如乔治亚理工学院 NSF-Simons 中心主任 Christine Heitsch 所说：“你不一定需要非常强大的数学来回答这些生物学问题，但你确实需要一位非常强大的数学家：一个能够理解这些问题，并提出关于它们的正确问题。”
迭代多尺度学习的过程。信用：周，P，王，S，李，T等人。通过多尺度随机动力学从单细胞转录组数据中剖析过渡细胞。纳通。 2021; 12, 5609。例如，UCI 中心的研究人员最近将自 1800 年代中期以来一直存在的数学流形理论应用于“细胞命运”，即对细胞及其未来身份的研究。 UCI 多尺度细胞命运研究中心 NSF-Simons 中心主任聂青领导的一个小组创建了一个动态流形，即具有山丘和山谷的 3D 表面，以模拟细胞命运。流形中的每个点都代表一个单独的细胞，山谷代表细胞类型。点附近流形的几何信息显示了干细胞将转变为特定细胞类型的概率。大多数生物学家永远不会学习流形理论，大多数数学家也不会关心细胞。 UCI 中心是开发这种了解细胞命运的新工具的关键。
同样在 UCI 中心，生物工程师 Tim Downing 和应用数学家 Elizabeth Read 一直在使用将随机性考虑在内的随机模型来检查细胞的表观遗传学。虽然细胞的遗传学指的是它的 DNA，但细胞的表观遗传学与 DNA 之上的东西有关：染色质或螺旋本身的形状，以及围绕它的分子。如果 DNA 是一个信息库，告诉细胞如何工作，那么表观基因组就是一个图书馆员，解释细胞需要哪些书籍或基因，哪些可以忽略。
虽然我们大多了解细胞在制造更多细胞时如何复制 DNA，但表观基因组仍然是一个谜。 Downing 在细胞周期过程中进行测量（一个细胞分裂成两个子细胞所需的时间），Read 在模拟潜在生物学机制的同时分析它们。他们一起发现，酶沿着 DNA 传播并按顺序构建表观基因组，而不是更分散地，一次完成。他们的发现暗示了染色质的形状：如果甲基化（一种改变 DNA 活性的生物过程）同时发生在两个不同的 DNA 区域，这表明这些位置在扭曲的 DNA 中是相邻的。
表观遗传机制受多种因素和过程的影响，包括子宫内和儿童期的发育、环境化学物质、药物和药物、衰老和饮食。图片来源：美国国立卫生研究院当数学和生物学相遇时，具有足够先验知识的两个领域都会出现偶然的理论。例如，在研究编码 RNA 结构的方法时，她发现了与经过充分研究的组合对象等效的东西。在 RNA 的背景下，这个对象更容易分析，她最终解决了组合学中的一个开放问题——如果没有生物学动机，她永远不会考虑这个问题。
后来，一名生物学专业的学生开始研究 Heitsch 的物体，并尝试使用图形或带有边缘的点集合来描述 RNA 折叠。学生认为他们可以列出所有可能的路径作为第一步，但 Heitsch 知道，由于图论中现有的数学，枚举将是一场计算噩梦。
“图论不是他们通常接触到的一种数学，”Heitsch 说，并指出许多生物学专业的学生只学习微积分。 “现在有各种各样的数学被用来分析生物学。如果你对生物学有足够的了解，你就会明白这样的数学是如何成为一个非常强大的工具的。我们已经成功地利用数学的可能性扩大了生物学家的视野。”
使生物学和数学的结合现代化
NSF-西蒙斯中心的最终目标是促进良性循环，实验生物学家的“湿实验室”的观察导致“干实验室”的新数学，然后刺激新的实验装置进行更多的“湿”实验。
例如，布劳恩开发了数学工具来搜索受昼夜节律影响的数千个基因的分子水平变化，继续进行一系列研究，通过确定所谓的果蝇的时钟基因。她合作的实验室在不同条件下每两小时测量一次果蝇的每个基因，持续 27-36 小时；然后，布劳恩的算法在嘈杂的数据中找到模式，寻找表现出周期性或与昼夜节律有关的基因。结合干湿数据，实验室弄清楚生物钟如何帮助果蝇适应环境变化。布劳恩非常尊重湿实验室以及“设计和执行这些实验需要多少知识、洞察力和直觉，以及你必须有多少耐心。”她哀叹“交易性”合作，并陶醉于她与生物学家合作者的关系。
“有些人只是希望完成统计数据，以便他们可以将其放入资助或论文中，而你再也不会讨论科学——这有点令人不快，”布劳恩说。 “归根结底，我喜欢来回交流，我们可以做一些分析，为不同的实验提出建议，并在实验和理论之间进行真正的对话。实验室现在正在进行的实验是我们深入参与设计的实验，因此我们能够将这些类型的方法应用于产生的数据。”
自从 Wigner 1960 年的原始论文以来，对这些实验和数据的测量有了突飞猛进的发展。在 1990 年代为人类基因组计划绘制基因图时，世界各地的科学家会用特定的荧光标记标记一两个基因或蛋白质，然后拍摄图像以查找基因组内的位置。如今，科学家们可以用空间单细胞基因组学一次标记所有 20,000 个左右的基因。这一令人印象深刻的壮举为数学生物学家提出了一个巨大的数据问题。令人高兴的是，数学具有识别和隔离相关信息的工具，弥合海量数据表之间的差距并弄清楚基因实际上在做什么。
Fefferman 解释说，借助新的分析方法、CRISPR 技术和更多“大数据”，数学生物学家可以从将更多机器学习和计算机工程工具纳入他们的工作中受益。
“在一个非常真实的意义上，为处理大数据的计算能力而开发的数学技术是一个令人难以置信的美丽挑战，”费弗曼说。 “这就像说，让我们拼出一个拼图游戏，但你一次只能随机获得 20 个拼图，而每次你放一个，你就会得到另一个。拼图有 50,000 块。”
NSF-西蒙斯中心的研究人员希望数学思维的严谨性和抽象性不仅有助于解决生物学难题，还能加速生物学发现。例如，正如奎南所说，一个具有同心圆行星轨道的地心宇宙是托勒密和其他人“一个合理的初步猜测”。当时的观察产生了本轮的概念，本轮用于准确预测行星在任何给定时间的位置，但没有深入了解它们是如何工作的，也不能扩展到新的物体。 “这不是一个糟糕的模型，”奎南说。 “这不是最好的。为了确保生物学不会满足于千百年来对生命的类似现象学理解，我们需要将生物学最好的部分与数学的最好部分结合起来。”
为避免被本轮等纯描述性理论误入歧途，这些理论无助于解释世界，研究人员希望将生物学和数学更紧密地结合在一起，以便他们能够理解如何从生物世界的公理中得出逻辑结论。
“我最担心的一个问题是，我们可以获取这些极其丰富的数据集，通过非常复杂的分析管道运行它们，并获得预测结果——但我们只是获得了非常好的本轮吗？”布劳恩说。 “现在，这是一个激动人心的时刻，因为它要求我们作为一个社区来思考这一点，并思考生物学的第一原理应该是什么样子。”