这是我最近遇到的一个奇怪的积分 [1]。
积分的存在有点令人惊讶,更令人惊讶的是它的值有一个简单的表达式。
这是被积函数的图。
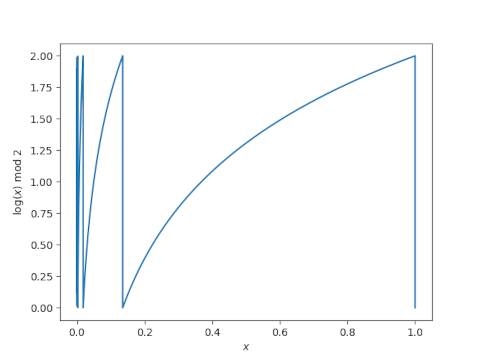
该情节并没有公正地对待左端的所有活动。当x趋向 0 时,左端堆积了无数个越来越垂直的线段。
如果您要在对数刻度上绘制被积函数,您会得到一个锯齿波,延伸到负无穷大。
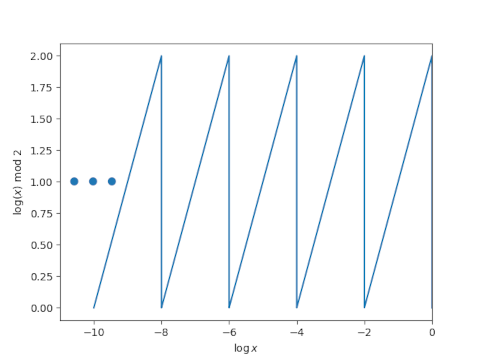
我预计如果不进行一些特殊处理,积分很难进行数值计算,但 SciPy 的quod函数默认情况下做得不错。
来自 numpy 导入日志,tanh 从 scipy.integrate 导入四元组 print(四元组(lambda x: log(x)%2, 0, 1)) 打印(1/tanh(1))
这会将积分计算为 1.313042…,而准确值为 1.313035…
值得赞扬的是,它在产生结果之前警告了困难:
IntegrationWarning:已达到最大细分数 (50)。
如果增加限制没有改善,建议分析被积函数以确定困难。如果可以确定局部困难的位置(奇异性、不连续性),那么人们可能会通过分割区间并在子范围上调用积分器而获益。也许应该使用专用积分器。
相关帖子
[1] 马修·A·尼埃米罗。自然对数模 2。美国数学月刊,卷。 128,第 2 期(2021 年 2 月),第 14 页。 177.
后对数锯齿首次出现在约翰·D·库克 (John D. Cook)身上。
原文: https://www.johndcook.com/blog/2025/04/12/logarithmic-sawtooth/