无论你从什么数字开始,如果你反复按计算器上的 cos 键,数字最终会停止变化。这个事实被无数玩计算器的孩子重新发现。
如果您从 0 开始(这可能是打开计算器时的默认值),那么您将在 90 步后达到最终值 [1]。您可以使用以下 Python 代码来验证这一点。
从数学导入 cos
x = 0
对于范围(100)内的 i:
x = 余弦 (x)
打印(i,x)
从迭代 90 开始,代码每次都会打印 0.7390851332151607。
可视化收敛
让我们使用蛛网图可视化值的序列。这是我四年前为一篇文章制作的图像,从x = 1 开始。
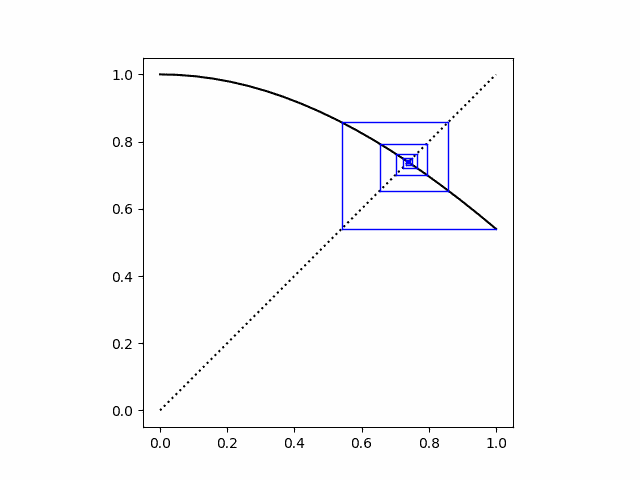
要阅读该图,请从水平轴上的x = 1 开始。黑色实线是余弦函数的图,因此蓝线起点高于 1 的点是y = cos(1) = 0.54。
由于我们要将输出重新转换为余弦作为输入,因此我们需要将y转换为x 。我们通过将点滑动到表示y = x 的虚线来实现此目的。这将创建水平蓝线,它是螺旋的第一段。这将我们带到了点 (cos(1), cos(1))。
现在,当我们再次取余弦时,我们得到 cos(cos(1)) = 0.86。现在,我们从之前的y = 0.54 值更改为新的y = 0.86 值。这给出了我们螺旋的下一段。我们再次需要将y转换为x ,因此我们像以前一样滑到线y = x ,只是这次我们是从左侧而不是右侧接近。
我们很快就到达了无法再看到收敛的地方。上图使用了 20 次迭代,最终在收敛点周围出现了一个蓝色斑点。
证明收敛性
我们说过迭代对于任何起点都是收敛的。这是为什么?
一方面,我们不妨假设x介于 0 和 1 之间;如果不是,则将在一次迭代之后。
中值定理表示对于 [0, 1] 中的任何对x 1和x 2 ,
cos( x 1 ) − cos( x 2 ) = − sin( c ) ( x 1 − x 2 )
对于 [0, 1] 中的某个c ,因为 cos( x ) 的导数是 − sin( x )。由此可见
| cos( x 1 ) − cos( x 2 ) | ≤ 罪(1) | x 1 − x 2 |
因为 sin( x ) 在 [0, 1] 上的最大值是 sin(1)。由于 sin(1) = 0.84… 小于 1,这表示余弦是 [0, 1] 上的收缩映射,因此存在一个不动点p使得 cos( p ) = p 。
收敛速度
我们可以用它来计算k 次迭代后x距固定点p 的距离的上限:
| x − p | ≤ sin(1) k
因此,如果我们想要位于固定点的距离 ε 之内,我们需要
k ≥ log(ε) / log(sin(1))。
这表示要获得定点的浮点精度(大约 10 -16 ),需要 214 次迭代。这是事实,但这是一个悲观估计,因为它基于 sin( c ) 的悲观估计。
一旦我们接近固定点p ,收敛速度就更像是 sin( p ) k而不是 sin(1) k 。这表明在大约 90 次迭代后我们应该在定点的浮点精度内,这就是我们在帖子顶部看到的。
更多定点柱
[1] 如果您的计算器使用64 位浮点数,则确实如此。如果您有一个精度较高或较低的计算器,您的里程可能会有所不同。
一遍又一遍地按余弦键的帖子首先出现在John D. Cook上。
原文: https://www.johndcook.com/blog/2024/12/17/cos-key-fixedpoint/