上一篇文章解释了为什么公历是这样的,并且它由整数周组成。由此可见,公历每 400 年重演一次。例如,2025 年的日历将与 1625 年和 2425 年的日历完全相同。
如果不在日历上打印年份,则只有 14 种可能的打印日历。元旦是星期几有七种可能,该年是否闰年有两种可能。
万年历是一组 14 种可能的日历,以及一些指示在给定年份适合哪种可能的日历的索引。
14 个日历中的每一个的出现频率都相同吗?不可以,因为日历中只有 400 年中的 97 年才会包含闰日。
每个非闰年日历的出现频率是否相同?不,因为有 303 个非闰年,而 303 不能被 7 整除。那么闰年日历呢?还是不能,因为 97 也不能被 7 整除。
现在我们可能期望在平年或闰年中,每个潜在日历的使用次数大约相同。但这是真的吗?下面是一些回答这个问题的 Python 代码。
普通计数 = [0]*7
跳跃计数 = [0]*7
y = 0 # 年模 400
跳跃计数[0] = 1
d = 0 自 1 月 1 日周期开始以来的 # 天
定义跳跃(y):
返回 y % 4 == 0 和 (y % 100 != 0 或 y % 400 == 0)
对于范围 (1, 400) 中的 y:
d += y*365
# 上一年是否是闰年
如果跳跃(y - 1):
d+=1
如果跳跃(y):
跳跃计数[d % 7] += 1
别的:
普通计数[d % 7] += 1
打印(普通计数)
打印(跳跃计数)
这是输出:
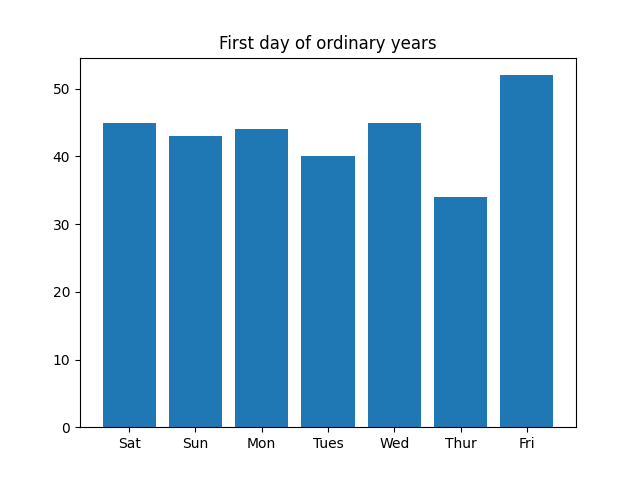
[45, 43, 44, 40, 45, 34, 52] [10, 11, 17, 16, 23, 13, 7]
日历类型的频率分布并不均匀。在闰年中,最常见的日历类型是最不常见类型的三倍多。
这是频率的条形图。图表从星期六开始,因为 2000 年 1 月 1 日是星期六。
一、平年:
然后,闰年:
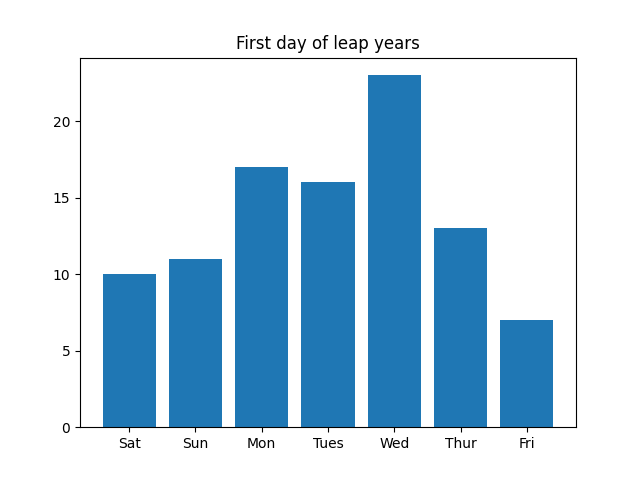
相关帖子
《万年历》一文首次出现在约翰·D·库克 (John D. Cook)上。
原文: https://www.johndcook.com/blog/2024/12/16/perpetual-calendars/