月塔#205 ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌

https%3A%2F%2Fsubstack.com%2Fimg%2Femail

这份时事通讯可能是垃圾

月亮塔#205

克里斯·阿卜杜勒梅西

11 月 5 日

在应用程序中阅读

朋友们，

我从来没有读过的 Substacks 之一是David Epstein的《Range Widely》 ，他是《Range》 （我对他采访这本书的笔记）和《运动基因：非凡运动表现科学内部》的作者。

大卫是一名记者。他的著作经过深入研究。社会科学研究，尤其是那种在机场书店里爬行的科普作品，应该需要“持保留态度”的评级（G：“germane”，PG：“可能是垃圾”，R：“传闻”最好”）。大卫的过程和理智的举止表明了他的谨慎——他抵制了过分夸大结论的诱惑。

就我个人而言，我很少读社会科学书籍——如果我关心的话，我只会听作者的播客。这类书中的见解让人感觉它们的收益不对称——如果它们证实了你已经想到的，那么阅读这本书的机会成本就很高（如果我在死之前再读 500 本书，我会很幸运）并且如果这本书有一个开创性的见解，它几乎肯定会在十年内过时（“在社会科学中发表的博弈论”是一个滑稽的分形想法。如果你用谷歌搜索这个短语，你就会明白为什么）。

不管怎样，大卫的智力关怀历史使他成为采访其他社会科学作者有关他们的书的理想人选——足够挑剔，可以提出好的问题，但也足够友好，可以让他首先获得采访。

序言已经足够了……我喜欢大卫与心理学家亚当·格兰特就他的新书《隐藏的潜力：实现更伟大的事情的科学》进行的问答（重点是我的）的一些摘录：

许多人认为，如果你不早熟，那就表明你缺乏潜力。但潜力并不在于你从哪里开始，而是在于你能走多远。最新的科学研究表明，我们不应该将速度误认为是能力。我们的学习速度是由动机和机会驱动的，而不仅仅是能力。想想那些大器晚成的人，他们没有足够幸运地偶然发现了自己的热情，或者没有很早就认识到并开发了他们隐藏的潜力的父母、老师或教练。

这并不意味着我们应该忽视“有天赋”的学生。我们也需要以不同的方式思考如何培养他们的潜力。根据经验，神童成为成年天才的比率出奇地低。我怀疑原因之一是他们学会了在别人的手艺上表现出色，却没有发展自己的手艺。掌握莫扎特的旋律并不能让你准备好创作自己的原创交响曲。 [克里斯：这正是特伦特·雷泽诺 (Trent Reznor)在与自己的潜力搏斗时向里克·鲁宾 (Rick Rubin) 提出的观点]。记住圆周率的数千位数字对于训练你的思维想出你自己的毕达哥拉斯定理几乎没有帮助。新技能越容易掌握，你面对失败的经验就越少。这是国际象棋大师莫里斯·阿什利（Maurice Ashley）给我上的一课：早期陷入困境的人往往会培养性格技能，以便日后脱颖而出。我们需要尽早开始投资于性格技能。
由于格伦妮是聋子，她必须找到非传统的学习方式，比如用身体的不同部位来感受与不同音高相对应的振动。她和她的老师一直在尝试不同的方法来做到这一点，并且用不同的方法来做每件事，真的。正如您所写：“不断改变任务并提高标准使学习成为一种乐趣。”我一直对可变练习这个问题着迷。不断地把事情混在一起似乎有悖常理，但事实证明这更有利于学习。
您注意到，在 40 岁时获得国际赞誉的音乐会钢琴家通常不会很早就着迷，而且他们对音乐的投入通常会缓慢但稳定地增加。这让我想起了《战歌》的第一页——作者在其中承诺了抚养典型成功孩子的秘诀，并讲述了给她女儿分配小提琴的故事，很快她就开始监督每天五个小时的刻意练习。这部分摘录在《华尔街日报》上，这是该报有史以来评论最多的文章！我认为它确实渗透到了公众意识中。没有给人留下太多印象的是书中后面的部分，作者（值得赞扬的是）讲述了她女儿转向她说：“你选择的，不是我的”，然后或多或少退出了。 [克里斯：由于这种“反应”，我会非常小心地让我们的孩子去他们自然会去的地方。我不想把“他们的事”变成“我的事”。你可以为那些你独立发现的东西提供额外的装备。]
“学习风格”的问题。这是一个非常流行的观点，即有些人通过听来学习最好，另一些人通过阅读来学习，另一些人通过看来学习，等等。也许有人更喜欢播客而不是书籍，因为他们将自己定位为“听觉学习者”。问题是，大量的研究未能支持这个想法[Kris：Veritasium 称这是“ 教育中最大的神话” 。尽管我怀疑驳回这一想法的实验的测试设计可能是对争论的草率处理或对它的解释过于狭隘]。

人们可能确实有一种感觉最舒服的学习方式，但这并不意味着他们实际上通过这种方式学到了更多东西。事实上，使用Range中的一行，在很多情况下，困难并不是你没有学习的标志，而是轻松是[ Kris：我发现很多我尊敬的老师都同意这一点，所以它并不那么大胆即使这是您第一次听到这种说法，也可能会出现这样的说法。我提醒我的孩子们——如果很简单，那就只是复习，而不是学习。非肤浅的学习会带来伤害。我什至可以说，学习和痛苦几乎是同义词。需要明确的是，这样的说法作为提醒比普遍真理更有用。体验式学习是一个简单的反例] 。正如您所写：“有时，您甚至在让您最不舒服的模式中学得更好，因为您必须更加努力。”我刚刚阅读了一项研究（“衡量实际学习与学习感觉”），该研究表明哈佛物理系的学生更喜欢高评价教师的讲座而不是主动学习练习。但他们从后者身上学到了更多。活跃小组的主要区别在于，学生必须在小组中尝试解决问题，然后才能真正知道自己在做什么，因此他们会在看到正确的解决方案之前进行讨论、提出问题并陷入死胡同。我们知道，强迫学习者在看到解决方案之前尝试生成解决方案可以增强学习效果（所谓的“生成效应”），但感觉不太好，所以我们可以避免这样做。
早在 12 月，你就帮我联系了 RA Dickey，他在采访中的表现正如你所承诺的那样出色。他的故事有助于解释为什么这么多人在陷入困境时未能尝试新方法。这并不是说我们固执或抵制改变。我们讨厌放弃已经取得的成果。我们有时忘记了，前进的最佳方式就是回到绘图板。 [Kris：感觉被看到了]如果你的快球速度变慢并且你的职业生涯停滞不前，那么修改指关节球不会给你带来任何损失。我们不应该因为害怕失败而不敢去尝试。

金钱角度

今天让我们抱怨一下房地产的现实。

当我看到那条推文和评论时，我的快速反应是：

这条推文遭到了很多人的讨厌，但是……这正是我为我购买的每个地方所做的。得到了同一家公司的代理人，这样他们就可以双倍投资。我的意思是，整个期权市场都围绕着了解双方计费的动态展开。

如果您是经纪商的常规客户，当对分割进行判断（通常是这样）时，您将获得更好的分配。每月几次放弃 5k 手数半美分的佣金，这样您就可以在 10k 手数上获得 1/2 而不是 1/4 的分配，一分钱一毛钱。

在期权世界中，分析和书呆子的东西受到了很多关注，但这也是最民主的方面。游戏的最高优势（尽管可扩展性最差）部分是关系维护。在由流行技术和捕食者/猎物种群划分所定义的时间快照内存在着针锋相对的平衡。技术或人口的巨大变化改变了平衡优序的参数。有一个常数——中间商“控制”流量。流是食物链底部的浮游生物。

我认为作为许多企业的比喻——人工智能将处理微积分。但是，接近那些早上醒来并提出导致他们买卖的观点的人永远是我们要做的工作。书呆子的东西很令人满意。但赚钱只是肮脏的工作。

拥有正确的期望很重要，以免当您发现谁赚了最多的钱（尤其是每单位风险）时您会哭泣。

[关于这个想法的先前即兴表演： 多汁的东西不会击中坑]

最后一件事……如果在我们启用 Zillow 的世界中 6% 的经纪商佣金持续存在让您感到困惑，那么时代似乎正在发生变化。最近的一项解决方案似乎是一个分水岭：

?中间人经济：为什么房地产经纪人遭受巨大损失而购房者可能受益（阅读 9 分钟）
作者：马特·斯托勒

陪审团针对全国房地产经纪人协会的价格操纵问题做出了一项令人震惊的 18 亿美元反垄断裁决，可能会重新调整房地产市场。

受虐狂的金钱角度

?新文章： 回报与波动性的简单演示

投注的预期回报是结果的简单概率加权平均值。
如果一个赌注有 50% 的机会获得 21% 的收益，并且有 50% 的机会获得 19% 的回报，那么这就是一个不错的赌注，而且不会波动。您期望平均赚取 20%（尽管事实上您不可能在任何单一投注中赚取这一金额，因为您只能赚取 19% 或 21%）。
一次尝试后您的预期最终财富是您开始时的 1.2 倍。
由于我们对结果进行了简单平均，我们计算出算术平均回报率为 20%

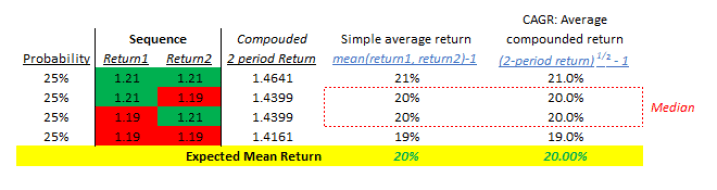
复合回报

对于不进行任何分配或“不予考虑的资金”的多期投资，我们无法使用简单的算术方法来计算预期回报。

尝试两次后考虑相同的赌注。以下是 4 种可能性，每种可能性均等：

最好的回报，最好的回报
最佳回报、最差回报
最差回报、最佳回报
最差回报，最差回报

如果我们看一下汇总表，平均预期回报率和中位数之间没有差异。

让我们保持平均回报相同，但增加波动性。一项投资同样可能：

上涨100%
下降60%

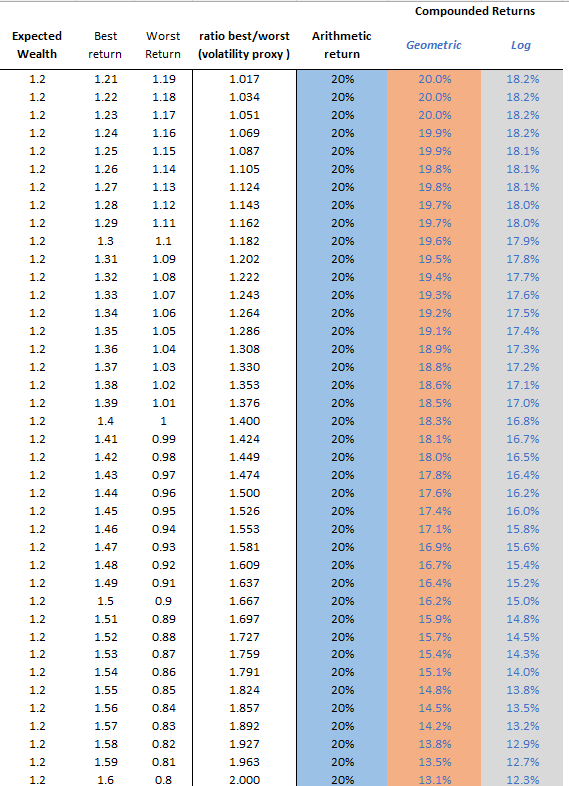
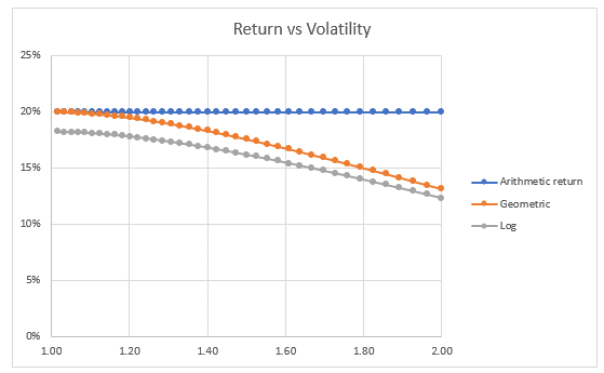
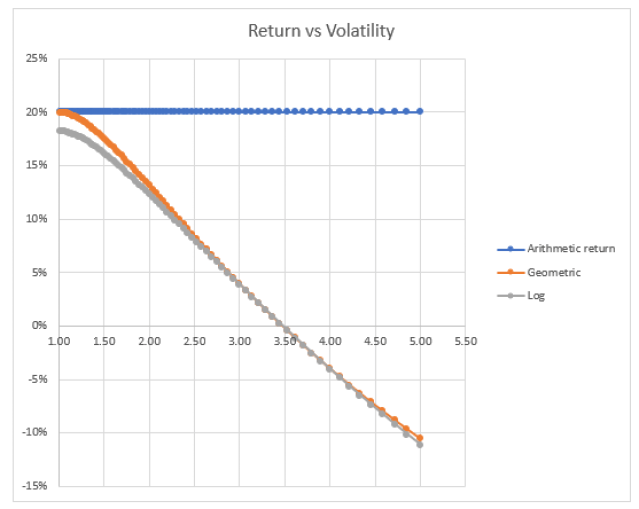
尽管这比第一次投资波动更大，但每次试验的平均预期回报率仍然为 20%。您可以通过两种方式计算：

50% * +100% + 50% * -60% = 20%

或者

终端财富 = 50% * 2 + 50% * .4 = 1.2 或 20% 回报

但是，让我们看看当我们考虑将第一期的收益完全重新投资到第二期的复合情景时会发生什么。

现在，平均复合回报率已从 20% 降至 4.72%，中值结果为损失 10.6%！

平均回报率和中位数回报率之间的差异来自于波动性的复合效应。

投资是一个乘法过程

当谈到投资时，我们通常会进行再投资，而不是每年将利润从桌面上拿走。我们希望我们的财富能够像这样逐年增长：

1.10 * 1.10 * 1.10 … 或 1.10 ⁿ其中 n 是复利间隔数（通常为年）。

因此，我们要关注的是复合回报率而不是平均回报率。为了计算它们，我们只需取终端财富的 n 次方根，其中 n 是年数。

如果您的资金在 5 年内翻倍，那么您的复合年增长率 = 2 ^1/5 – 1 = 14.9%

请注意，如果您采用朴素平均回报率，您可以说您在 5 年内赚取 100% 或每年赚取 20%。但这与每年重新投资越来越多的资本的现实背道而驰。

CAGR是回报中位数

值得注意的是，这些投资的预期平均回报率仍然是每年 20%。只是中位数要低得多。在高波动性示例中，您的生活经历通常会导致 10.6% 的损失，但平均2 期回报仍然为正 4.7%。复杂的是，平均数是由您连续 2 年将资金翻倍的 25% 的概率驱动的。在所有其他情况下，你都会赔钱。

波动性正在改变结果的分布，而不是平均结果。

从数学上讲，中位数是几何平均数。在乘法过程中，您更关心几何平均值。毕竟，你只有一次生命。

关于日志返回的注释

对数回报是复合回报，我们假设连续复利。因此，与其说是每年，不如说是每秒。当然，如果我们的财富在 5 年内从 1 美元增长到 2 美元，但我们假设计算间隔很小，那么每个间隔的比率一定很小。毕竟我们旅程的起点和终点（1 美元到 2 美元）是相同的，我们只是将其切成更小的部分。

计算预期的对数回报很简单。使用易失性示例：

.5 * ln(2) + .5 + ln(.40) = -11.2%

请注意，这比我们之前计算的 -10.6% 的几何平均回报率（又称中位数）稍差

波动性对复合收益的影响

下表列出了不同的投资，每种投资的预期算术回报率为 20%。就像上面的例子一样。但不同的收益会被改变以代表不同程度的波动性。即使平均回报相同，一项可赚取 21% 或 19% 的投资的波动性也比可回报 100% 或 -60% 的投资要小得多。

我们使用最简单的衡量标准来表示波动性——最佳回报与最差回报的比率。

稳定投资波动率代理为1.21 / 1.19 = 1.017

上述投资波动率为 2 / .4 = 5.00

表片段：

这些图表显示了当我们增加波动性（最佳回报与最差回报之比）时算术回报和中值回报之间的差异：

一项投资回报 60% 的可能性与损失 20% 的可能性相同，其预期回报率为 20%，但如果您继续进行再投资，您的长期中值结果将接近 12-13% 的复合年增长率。

如果我们将波动率进一步提高到 5 倍（终端财富 2 倍与 0.4 倍）会怎样：

当比率为 3.5（1.87x 与 0.53x）时，我们的中值结果为零。当比率为 5 时，平均回报率仍为 20%，但中值回报率下降了 10%。几乎所有的路径都在失去，它们只是被你不断翻转头的不太可能发生的事件所抵消。

要点

投资是一个乘法过程，因此我们希望关注复合或对数回报，而不是简单回报
复合回报问“从一个时期到另一个时期的增长率是多少，才能让我们从起点到终点？”
复合和对数返回始终小于算术返回
复合回报和对数回报是衡量波动性造成损失后您期望在银行账户中找到的内容的更好指标。请记住，如果您的投资损失了 50%，您需要 100% 才能恢复平衡。如果您的投资收益为 50%，则只需损失 33% 即可收回成本。
如果没有波动性，就没有回报的承诺，但波动性是对回报的二次拖累。您的投资组合的最佳点可能属于广泛多元化投资组合的波动范围。通过重新平衡，您可以降低集中风险，避免将您的全部储备金变成硬币。即使这枚硬币有积极的预期，请记住你不能吃理论上的优势。