![]()
介绍
在另一篇文章中,我们阐述了 $SO(3)$ 的不可约表示,其中我们发现自己正在研究球体上的调和多项式。在这篇文章中,我们研究了 $SO(3)$ 的另一类表示,它在物理学中有其自身的意义:投影表示。结果将写为 $SU(2)$ 的不可约表示的直和,因此建议读者查看相应的帖子。我们记得
$SU(2)$ 的每个不可约酉不可约表示的形式为 $V_n$,其中
表示论在物理学中有十亿个应用。群 $SO(3)$ 以一种明显的方式充当 $\mathbb{R}^3$ 中的方向保持正交对称群。这种作用下的不变性证明了物理反应(例如基本粒子之间的反应)不应该取决于观察者的有利位置的原理。
然而,表示论在物理学中的应用并不仅限于有限维向量空间。撇开无限维向量空间不谈,有时我们还需要一类向量来代替单个向量。例如,给定一个波函数 $\psi$,我们知道 $|\psi|^2$ 可以解释概率密度。但是对于任何 $\lambda \in S^1$,我们看到 $|\lambda\psi|^2=|\psi|^2$,因此 $\lambda\psi$ 和 $\psi$ 应该等价于一种感觉。通过考虑这些等价类,我们发现自己在考虑射影空间。因此考虑投影表示是有意义的
其中 $G$ 是紧凑的。在这篇文章中,我们将假设 $G=SO(3)$ 并看看我们能走多远。
参数的简化
我们从一个简单的群论引理开始:
引理 1.一个有
其中 $C_n$ 是第 $n$ 个单位根的组,通过映射 $\xi \to \xi I$ 嵌入到 $SL(n,\mathbb{C})$ 中。
证明。考虑规范映射
这张地图是满射的。对于任何 $B\mathbb{C}^\ast \in GL(n,\mathbb{C})/\mathbb{C}$,我们有 $B\mathbb{C}^\ast=\frac{1} {|B|}B\mathbb{C}^\ast$,$\frac{1}{|B|}B \in SL(n,\mathbb{C})$ 是 $B\mathbb 的原像{C}^\ast$。
另一方面,我们看到 $\ker p$ 由 $SL(n,\mathbb{C})$ 中的标量矩阵组成。如果$\lambda I \in SL(n,\mathbb{C})$,则$|\lambda I|=\lambda^n=1$,从而$\ker p$可以被识别为$C_n$,证明同构。 $\平方$
因此,在研究射影表示$G \to PGL(n,\mathbb{C})$时,我们很快就被简化为特殊的线性群,这就简单多了。此外,第 n 个单位根的群比非零复数群简单得多。
然而,我们的简化并没有走到尽头。接下来我们将看到特殊线性群可以简化为特殊酉群。回想一下,紧李群的线性矩阵表示类似于酉群。以下引理是一个射影类比。
引理 2.设 $G$ 为紧李群。每个同态 $\varphi:G \to PGL(n,\mathbb{C})=SL(n,\mathbb{C})/C_n$ 与一个同态共轭,其图像位于 $SU(n)/C_n$ .
证明。考虑 $G$ 和 $SL(n,\mathbb{C})$ 在 $PGL(n,\mathbb{C})$ 上的纤维乘积 $ H$:
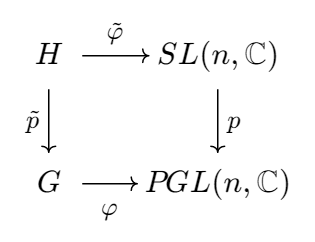
这里,$p$ 是 $SL(n,\mathbb{C}) \to SL(n,\mathbb{C})/C_n$ 的规范投影。这足以表明 $\tilde\varphi$ 类似于酉表示。明确地,一个有
与 $\tilde\varphi:(g,A) \mapsto A$ 和 $\tilde{p}:(g,A) \to g$。由于 $G$ 是紧致的并且 $\tilde{p}$ 具有有限核 $C_n$,因此可以看出 $H$ 是紧致李群。因此,矩阵表示 $\tilde\varphi:H \to SL(n,\mathbb{C})$ 类似于同态 $H \to SU(n)$,由此得出引理。 $\平方$
因此我们只能考虑同态
为了这篇文章。但我们还没有完成。不得不处理商群无论如何都不能令人满意。
由于 $SU(n)$ 是单连通的(见此视频),投影 $SU(n) \to SU(n)/C_n$ 是通用覆盖。特别地,当 $n=2$ 时,我们看到 $SU(2) \to SU(2)/C_2 = SO(3)$ 是我们众所周知的通用覆盖。如果我们将 $\varphi$ 提升到通用覆盖,我们看到自己正在处理 $SU(2) \to SU(n)$。准确地说,我们有如下的交换图(万能覆盖是一个函子):
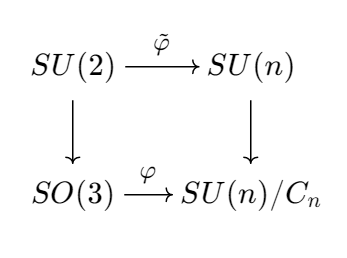
处理 $\tilde\varphi$ 就简单多了。物理学家对四元数群 $SU(2) = \operatorname{Spin}(3)$ 的酉表示比 $SO(3)$ 更感兴趣,尽管它看起来更自然。
发现射影表征
现在我们有兴趣找到所有可以下推到 $SO(3)$ 的射影表示的酉表示。我们有两个问题:
问题 1.考虑 $\tilde\varphi:SU(2)\to SU(n)$ 形式的映射是否足够?
答案是肯定的。请注意,每个同态 $f:SU(2) \to U(1)$ 都必须是平凡的。如果不是,则 $\ker f$ 应该是 $SU(2)$ 的非平凡真正规子群,即它必须是 $C_2$。但是 $SU(2)/C_2 \cong SO(3)$。一个矛盾。
还记得确切的顺序
设 $g:SU(2) \to U(n)$ 是任何同态,并考虑规范投影 $\pi:U(n) \to \frac{U(n)}{SU(n)}=U (1)$。我们看到 $\pi \circ g$ 将 $SU(2)$ 中的任何元素发送到 $1$,这意味着 $SU(2)$ 在 $U(n)$ 中的图像必须在 $SU(n)$ 中。因此,通过考虑 $SU(2) \to SU(n)$ 形式的映射,我们没有遗漏任何东西。 $\平方$
问题 2.为了确定 $\tilde\varphi:SU(2) \to SU(n)$ 是否可以下推到态射 $\varphi:SO(3) \to SU(n) 应该考虑什么/C_n$?
答案是,应该考虑元素 $-I$。令 $p:SU(2) \to SO(3)$ 为通用覆盖,令 $p_n:SU(n) \to SU(n)/C_n$ 为相应的通用覆盖。对于 $\tilde\varphi:SU(2) \to SU(n)$,我们想知道什么时候会有一个同态 $\varphi:SO(3) \to SU(n)/C_n$ 使得 $p_n \circ \tilde\varphi = \varphi \circ p$。
注意 $p(-I)=I$,因此,如果 $\varphi$ 存在,则有 $p_n \circ \tilde\varphi(-I)=e$,即群 $SU(n)/ 中的恒等式C_n$,因为应该有 $\varphi(I)=e$。因此 $\tilde\varphi(-I) \in \ker p_n$。因此 $\varphi(-I)$ 可以被识别为第 n$ 个单位根。由于 $\tilde\varphi(-I)\tilde\varphi(-I)=\tilde\varphi(I)$,我们看到 $\tilde\varphi(-I)$ 也应该被识别为 $1 的平方根$。也就是说,$\tilde\varphi(-I)$ 是 $\operatorname{id}$ 或 $-\operatorname{id}$。我们在以下问题中讨论这两种情况。
另一方面,如果 $\tilde\varphi(-I)=\pm\operatorname{id}$,那么可以验证 $p_n \circ \tilde\varphi \circ p^{-1}$ 可以很好-定义。因此 $\tilde\varphi$ 可以被推入 $SO(3)$ 的态射当且仅当 $\tilde\varphi(-I)=\pm\operatorname{id}$。 $\平方$
问题 3.设 $W=\bigoplus_n k_n V_n$ 是 $SU(2)$ 的表示。如果它可以被推低为 $SO(3)$ 的投影表示,会发生什么?
设 $\tilde\varphi:SU(2) \to SU(n)$ 是对应于 $W$ 的同态。我们已经确定当且仅当 $\tilde\varphi(-I)=\pm\operatorname{id}$ 时 $\tilde\varphi$ 可以被下推到 $SO(3)$。
如果 $\tilde\varphi(-I)=\operatorname{id}$,那么所有的 $n$ 都必须是偶数,因为当 $n$ 是奇数时,对多项式的操作不能是恒等式。如果 $\tilde\varphi(-I)=-\operatorname{id}$,那么所有的 $n$ 都必须是奇数,因为当 $n$ 是偶数时 $-I$ 对多项式的作用必须是恒等式.
更明确地说,$W=\bigoplus_n k_{2n}V_{2n}$ 或 $W=\bigoplus_{n}k_{2n+1}V_{2n+1}$。
定理 1. $SO(3)$ 的射影表示给出了 $SU(2)$ 形式的共轭
取决于 $(-I)$ 是 $\operatorname{id}$ 还是 $-\operatorname{id}$ 。
简而言之,在考虑 $SO(3)$ 的投影表示时,人们会考虑两个变量的多项式,这两个变量的项要么全为偶数,要么全为奇数。
在研究 $\tilde\varphi:SU(2) \to SU(n)$ 时,我们看到 $\tilde\varphi(-I)$ 可以被识别为第 n$ 个单位根和统一。然而,当 $n$ 为奇数时,我们看到 $\tilde\varphi(-I)$ 不能被识别为 $-1$,即 $-I$ 不能充当 $-\operatorname{id}$。出乎意料的是,数论在这里发挥了很小的作用。