你好!我一直在考虑写一本关于事物在计算机上如何以字节表示的杂志,所以我在考虑浮点数。
关于浮点运算的危险,我已经听过一百万次了,比如:
- 加法不结合(0.1 + 0.2 不同于 0.2 + 0.1)
- 如果您将非常大的值添加到非常小的值,您可能会得到不准确的结果(小数字会丢失!)
- 你不能将非常大的整数表示为浮点数
- NaN/无穷大值可以传播并导致混乱
- 有两个零(+0 和 -0),它们的表示方式不同
- 非正规/次正规值很奇怪
但我发现所有这些本身有点抽象,我真的想要一些实际程序中浮点错误的具体例子。
所以我在 Mastodon 上询问了浮点数在实际程序中是如何出错的例子,并且一如既往地提供了!这里有一堆例子。我还为其中的一些编写了一些示例程序,以查看到底发生了什么。这是目录:
- 示例 1:停止的里程表
- 示例 2:Javascript 中的推文 ID
- 示例 3:方差计算出错
- 示例 4:不同的语言有时会以不同的方式执行相同的浮点计算
- 示例 5:深空海妖
- 示例 6:不准确的时间戳
- 示例 7:将页面拆分为多列
- 示例 8:碰撞检查
这 8 个示例都没有讨论 NaN 或 +0/-0 或无穷大值或次正规,但这并不是因为这些东西不会导致问题——只是我在某个时候厌倦了写作 :)。
另外,我可能在这篇文章中犯了一些错误。
浮点数是如何工作的?
我不打算在这篇文章中详细解释浮点数的工作原理,但这是我几年前写的一篇漫画,它讨论了基础知识:
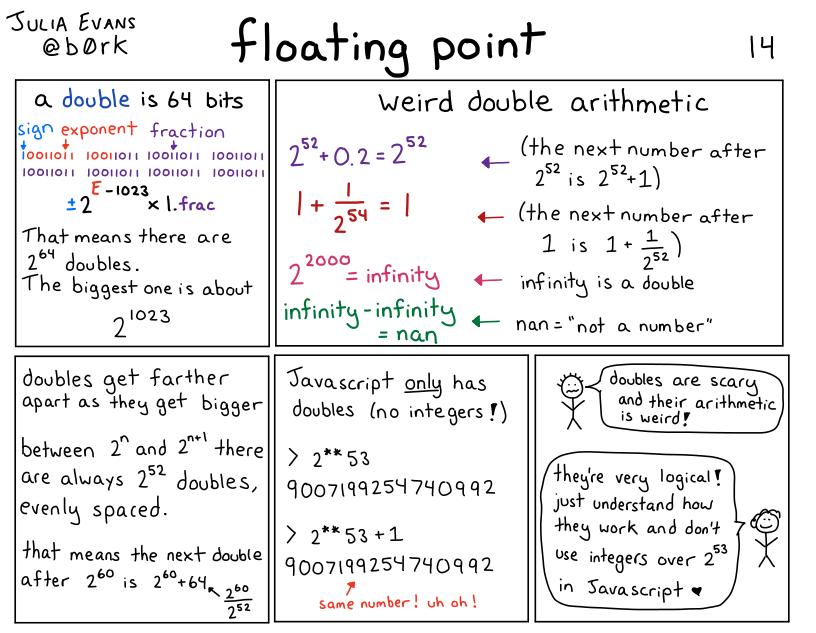
现在让我们进入示例。
示例 1:停止的里程表
一个人说他们正在研究一种里程表,该里程表不断将少量数据添加到 32 位浮点数以测量行驶的距离,但事情变得非常不对劲。
为了具体说明,假设我们每次向里程表添加 1 厘米的数字。 10000公里后是什么样子?
这是一个模拟它的 C 程序:
#include <stdio.h> int main() { float meters = 0; int iterations = 100000000; for (int i = 0; i < iterations; i++) { meters += 0.01; } printf("Expected: %f km\n", 0.01 * iterations / 1000 ); printf("Got: %f km \n", meters / 1000); }
这是输出:
Expected: 10000.000000 km Got: 262.144012 km
这非常糟糕——这不是一个小错误,262 公里比 10,000 公里少很多。什么地方出了错?
出了什么问题:浮点数之间的差距变大
本例中的问题是,对于 32 位浮点数,262144.0 + 0.1 = 262144.0。所以不仅仅是这个数字不准确,它实际上根本不会增加!如果我们再行驶 10,000 公里,里程表仍将停留在 262144 米(又名 262.144 公里)。
为什么会这样?好吧,浮点数变得越来越大。在此示例中,对于 32 位浮点数,这里有 3 个连续的浮点数:
- 262144.0
- 262144.03125
- 262144.0625
我通过访问https://float.exposed/0x48800000并将“重要”数字递增几次来获得这些数字。
因此,262144.0 和 262144.03125 之间没有 32 位浮点数。为什么这是个问题?
问题是 262144.03125 大约是 262144.0 + 0.03。因此,当我们尝试将 0.01 添加到 262144.0 时,四舍五入到下一个数字是没有意义的。所以总和保持在 262144.0。
另外,262144 是 2 的幂(2^18)也不是巧合。浮点数的差距在每次 2 的幂后发生变化,在 2^18 处,32 位浮点数之间的差距从 0.016 增加到 0.03125。
解决这个问题的一种方法:使用双
使用 64 位浮点数可以解决这个问题——如果我们在上面的 C 程序中用double精度数替换float ,一切都会好很多。这是输出:
Expected: 10000.000000 km Got: 9999.999825 km
这里仍然存在一些小的误差——我们偏离了大约 17 厘米。这是否重要取决于上下文:如果我们正在进行精确的太空机动或其他事情(例如在这次由浮点数学引起的导弹灾难中),稍微偏离很可能是灾难性的,但对于里程表来说可能没问题。
另一种改进方法是将里程表分块增加——而不是一次增加 1 厘米,也许我们可以降低更新频率,比如每 50 厘米更新一次。
如果我们使用 double并增加 50 厘米而不是 1 厘米,我们会得到完全正确的答案:
Expected: 10000.000000 km Got: 10000.000000 km
示例 2:Javascript 中的推文 ID
Javascript 只有浮点数——它没有整数类型。可以用 64 位浮点数表示的最大整数是 2^53。
但是推文 ID 是很大的数字,大于 2^53。 Twitter API 现在将它们作为整数和字符串返回,因此在 Javascript 中你可以只使用字符串 ID(如“1612850010110005250”),但如果你试图在 JS 中使用整数版本,事情就会变得非常错误。
您可以通过获取推文 ID 并将其放入 Javascript 控制台来自行检查,如下所示:
>> 1612850010110005250 1612850010110005200
请注意,1612850010110005200 与 1612850010110005250 不是同一个数字!!少了50!
这个特殊问题不会发生在 Python(或我所知道的任何其他语言)中,因为 Python 有整数。如果我们在 Python REPL 中输入相同的数字,会发生以下情况:
In [3]: 1612850010110005250 Out[3]: 1612850010110005250
与您预期的相同。
示例 2.1:损坏的 JSON 数据
这是“Javascript 中的推文 ID”问题的一个小变体,但即使您实际上没有编写 Javascript 代码,JSON 中的数字有时仍会被视为浮点数。这对我来说很有意义,因为 JSON 的名称中有“Javascript”,因此按照 Javascript 的方式解码值似乎是合理的。
例如,如果我们通过jq传递一些 JSON,我们会看到完全相同的问题:数字 1612850010110005250 变为 1612850010110005200。
$ echo '{"id": 1612850010110005250}' | jq '.' { "id": 1612850010110005200 }
但它在所有 JSON 库中并不一致 Python 的json模块会将1612850010110005250解码为正确的整数。
一些人提到了在 JSON 中发送浮点数的问题,无论是他们试图在 JSON 中发送一个大整数(如指针地址)并且它被损坏,还是反复来回发送较小的浮点值并且该值随着时间慢慢发散.
示例 3:方差计算出错
假设您正在做一些统计,并且您想要计算许多数字的方差。可能比您可以轻松地容纳在内存中的数字更多,因此您想一次性完成。
这篇博文中有一个简单(但不好!!!)的算法,您可以使用它来计算单次传递中的方差。这是一些 Python 代码:
def calculate_bad_variance(nums): sum_of_squares = 0 sum_of_nums = 0 N = len(nums) for num in nums: sum_of_squares += num**2 sum_of_nums += num mean = sum_of_nums / N variance = (sum_of_squares - N * mean**2) / N print(f"Real variance: {np.var(nums)}") print(f"Bad variance: {variance}")
首先,让我们使用这个糟糕的算法来计算 5 个小数的方差。一切看起来都不错:
In [2]: calculate_bad_variance([2, 7, 3, 12, 9]) Real variance: 13.84 Bad variance: 13.840000000000003 <- pretty close!
现在,让我们试试相同的 100,000 个非常接近的大数(分布在 100000000 和 100000000.06 之间)
In [7]: calculate_bad_variance(np.random.uniform(100000000, 100000000.06, 100000)) Real variance: 0.00029959105209321173 Bad variance: -138.93632 <- OH NO
这是非常糟糕的:不仅是差的方差,而且是负的! (方差永远不应该是负数,它总是零或更多)
出了什么问题:灾难性的取消
这里发生的事情类似于我们的里程表数字问题: sum_of_squares数字变得非常大(大约 10^21 或 2^69),并且在这一点上,连续浮点数之间的差距也非常大 – 2**46 .所以我们只是在计算中失去了所有的精度。
这个问题的术语是“灾难性抵消”——我们要减去两个非常接近的非常大的浮点数,这不会给你正确的答案。
我之前提到的博客文章讨论了人们用来计算方差的更好算法,称为 Welford 算法,它没有灾难性的取消问题。
当然,大多数人的解决方案是只使用像 Numpy 这样的科学计算库来计算方差,而不是尝试自己做:)
示例 4:不同的语言有时会以不同的方式执行相同的浮点计算
一堆人提到不同的平台会以不同的方式进行相同的计算。这在实践中出现的一种方式是——也许您有一些前端代码和一些后端代码执行完全相同的浮点计算。但它在 Javascript 和 PHP 中的做法略有不同,因此您的用户最终会看到差异并感到困惑。
原则上你可能认为不同的实现应该以相同的方式工作,因为 IEEE 754 浮点标准,但这里有几个提到的警告:
- libc 中的数学运算(如 sin/log)在不同的实现中表现不同。因此,使用 glibc 的代码可能会为您提供与使用 musl 的代码不同的结果
- 某些 x86 指令可以在内部对某些双精度运算使用 80 位精度而不是 64 位精度。这是一个关于这个的 GitHub 问题
我对这些要点不是很确定,也没有可以重现的具体示例。
示例 5:深空海妖
Kerbal Space Program 是一款太空模拟游戏,它曾经有一个名为Deep Space Kraken的错误,当你移动得非常快时,你的船会由于浮点问题而开始被摧毁。这类似于我们讨论过的涉及大浮点数的其他问题(如方差问题),但我想提及它是因为:
- 它有一个有趣的名字
- 这似乎是视频游戏/天体物理学/一般模拟中的一个非常常见的错误——如果你的点离原点很远,你的数学就会搞砸
另一个例子是 Minecraft 中的边境之地。
示例 6:不准确的时间戳
我保证这是“非常大的浮点数会毁了你的一天”的最后一个例子。但!还有一个!假设我们尝试将当前 Unix 纪元(以纳秒为单位)(大约 1673580409000000000)表示为 64 位浮点数。
这可不行! 1673580409000000000 大约是 2^60(重要的是,大于 2^53),它之后的下一个 64 位浮点数是 1673580409000000256。
所以这将是一个很好的方法来结束你的时间数学不准确。当然,时间库实际上将时间表示为整数,所以这通常不是问题。 (始终存在2038 年问题,但这与花车无关)
一般来说,这里的教训是,如果可以的话,最好使用整数。
示例 7:将页面拆分为多列
既然我们已经讨论了大浮点数的问题,那么让我们做一个小浮点数的问题。
假设您有一个页面宽度和一个列宽,并且您想计算出:
- 多少列适合页面
- 剩下多少空间
您可以合理地尝试floor(page_width / column_width)作为第一个问题,而page_width % column_width作为第二个问题。因为这对整数来说工作得很好!
In [5]: math.floor(13.716 / 4.572) Out[5]: 3 In [6]: 13.716 % 4.572 Out[6]: 4.571999999999999
这是错误的!剩余空间量为0!
计算剩余空间量的更好方法可能是13.716 - 3 * 4.572 ,这给了我们一个非常小的负数。
我认为这里的教训是永远不要用浮点数以两种不同的方式计算同一件事。
这是一个非常基本的示例,但如果我使用浮点数进行页面布局或进行 CAD 绘图,我可以看出这将如何产生各种问题。
示例 8:碰撞检查
这是一个非常愚蠢的 Python 程序,它从 1000 开始一个变量并递减它直到它与 0 碰撞。你可以想象这是乒乓球游戏或其他东西的一部分,并且a是一个应该与墙碰撞的球。
a = 1000 while a != 0: a -= 0.001
您可能希望该程序终止。但事实并非如此! a从不为 0,而是从 1.673494676862619e-08 到 -0.0009999832650532314。
这里的教训是,通常您不需要检查浮点数是否相等,而是要检查两个数字是否相差非常小。或者在这里我们可以只写while a > 0 。
目前为止就这样了
我什至没有接触到 NaN(它们太多了!)或无穷大或 +0 / -0 或次正规,但我们已经写了 2000 字,我打算发表这个。
稍后我可能会写另一篇后续文章 – Mastodon 线程中确实有 15,000 个单词的浮点问题,有很多材料!或者我可能不会,谁知道 🙂
原文: https://jvns.ca/blog/2023/01/13/examples-of-floating-point-problems/