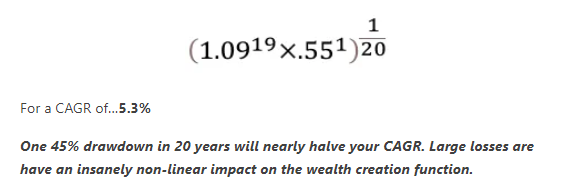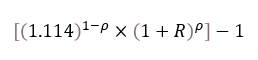月塔 #211 ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌‌ ‌‌‌‌

转发此电子邮件？在这里订阅以了解更多信息

风险取决于解决方案

月亮塔#211

克里斯·阿卜杜勒梅西

1月7日

在应用程序中阅读

朋友们，

在新年的第一个周日，我想为 2024 年发布一篇简短而有用的帖子：

比看起来更难（5 分钟阅读）
贾里德·迪里安

简短而甜蜜的台词：

我没有反应，因为我不是动物。

几乎两年前，我制作了一个充满同样精神的推文版本。我们称之为停车场同理心：

金钱角度

我对我上一篇文章《长痘飞机》的投资部分感到失望。让我们用它来解决这个问题，看看我们的结果如何。

回顾：

a) 我们回顾了波动率（一阶数量）如何以非线性方式“拖累”中值回报

波动率项阻力是平方项。从另一个角度可以理解同样的直觉 – 如果你损失了 X%，你需要重新获得 X/(1-X)，你可以在你值得信赖的 TI-82 中绘制它，看看它是非线性的。

损失 10%，你需要赚 11% 才能恢复平衡。
损失33%，需要获得50%。
失去50%，需要获得100%。
失去75%，需要获得300%

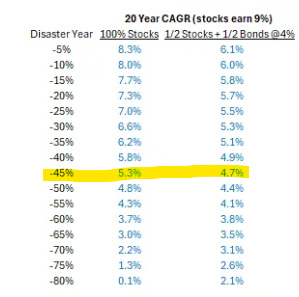
b) 我展示了为什么大幅回撤对复合年增长率产生巨大影响

我的玩具示例假设 19 年的复合回报率为 9%，然后回撤 45%。

c) 在这种情况下，如果您将 50% 投资于股票，将 50% 投资于债券，则您的情况大致相同，收益率为 4%

当我点击发送时，我开始感到奇怪。我做了一些偷懒的事。问题变得更糟，因为我收到了 3 条来自人们的消息，他们说这是他们见过的最好的东西之一，因为它证实了直觉，但没有看到它以这种方式呈现。但它有一个问题。事实上，我告诉一位读者给我打电话，因为我想解释为什么需要修改。

因此，作为一个小测试，问问自己问题是什么？（这也不是税收问题）。

好吧，让我们开始思考过程和解决方案。

我最初选择 9% 是因为我想要一个我们集体良心一致认为的复合年增长率，这是对长期股票指数复合年增长率的合理猜测。

问题是我不能在 20 年中的 19 年中使用 9%，因为 20 年复合年增长率需要约为 9%，包括回撤！我们对股市回报的看法已经包括了所有可怕的时期。我不能只使用复合年增长率，然后就减少 45%。

相反，我需要：

为这 19 年选择一个高于 CAGR 的数字
应用 45% 的回撤
确保 20 年复合年增长率为 9%

一旦我到达这一点，我就通过https://www.officialdata.org/us/stocks/sp-500/1900查找自 1926 年以来 SP500 月度回报率（SP500 指数当时还不存在，但自那以后）他们将此基于罗伯特希勒的工作（我只是假设历史重构是有效的）。

使用月度数据时，数据集包括 1161 个 12 个月的滚动回报。我们发现：

年度简单（算术）回报 11.4%
年复合增长率：10.2%
年化波动率：15.4%
这些回报中的 0.50%（即 200 分之一）包括 45% 或以上的 12 个月损失

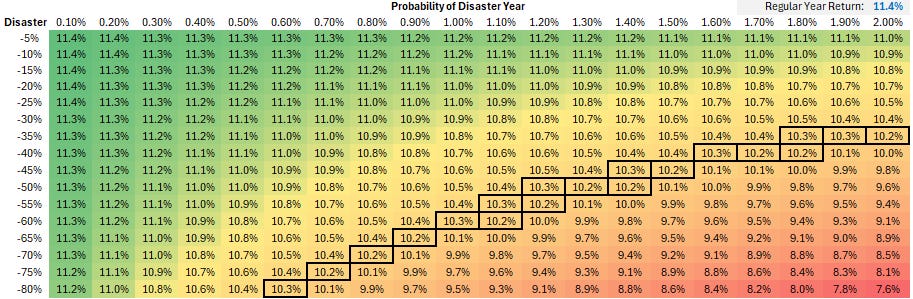
在上一篇文章中，我假设灾难年份发生的概率为十分之一，但从历史角度来看，这一概率比按月分辨率测量的概率要小得多。

我重新进行了计算，假设典型年份的回报率为 11.4%，并允许 2 个变量发生变化：

灾年回归(R)
发生灾难的概率 (p)

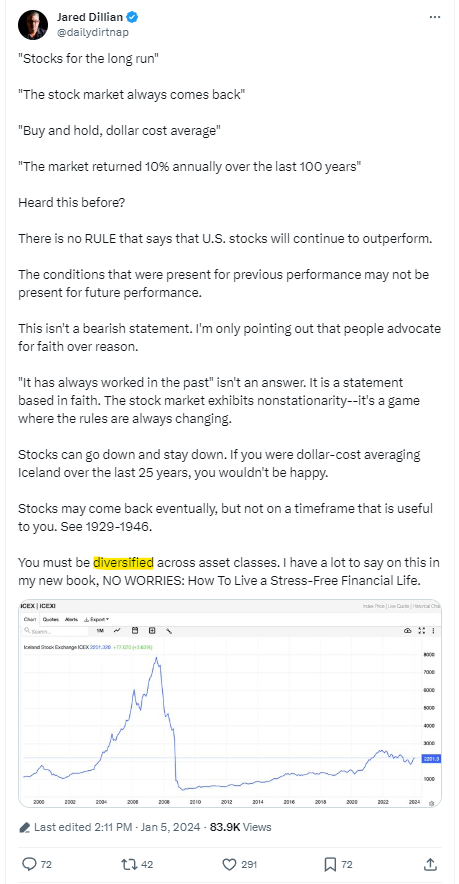
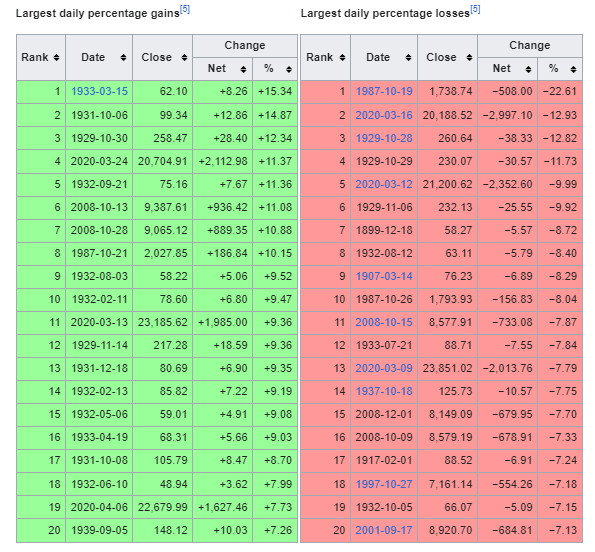
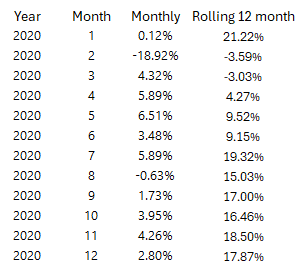
每个单元格中的公式为：

表输出：

（重点关注复合年增长率约为 10.2% 的细胞）

这不是股票模拟，因此 11.4% 的假设回报率只能被视为扣除波动性后的复合回报率。这隔离了 12 个月 R 下降对概率 p 的影响，只是为了看看总 CAGR 有多敏感。

直到 45% 的灾难以 50 分之一到 200 年 1 分之一的比例发生时，复合年增长率才可能下降整整 1%。

这可能会让读者现在冲到船的另一边……“嘿，将 100% 投入股票是个好主意”

但请记住，美国股市的历史样本量很小。真实的样本量需要查看非重叠收益，而不是滚动 12 个月的收益。这意味着您可以获得与几年一样多的数据点。

而且这只是美国。

贾里德再次出现（我读他的书已经十年了……他的个人理财书很快就会出版，这条推文对于这篇文章来说是及时的）：

但让我在讨论中添加一个数学点……查看月度回报隐藏了情感路径以及分布知识。

让我解释。标准差是标准化的度量。它们的移动大小随时间变化。

苏格拉底式的论证：

股指1年内下跌10%的可能性更大还是1天内下跌10%的可能性更大？

这很容易，当然是一年之内。但回报本身并未随时间标准化。这只是一个原始数字……10%

让我们换个方式问这个问题。

股市1天内下跌3个标准差的可能性更大还是1年内下跌3个标准差的可能性更大？

您现在应该选择 1 天。

可以这样想……1987 年，股市一天内下跌了 20% 以上。我不知道 SP500 的波动性是什么导致了崩盘，但如果每日标准差超过 3%，我会感到惊讶。那天会有 7 个标准差。

您从未见过 1 年 7 标准差的变动。

道指单日最大涨幅：

维基百科

使用之前的重叠数据，我们发现 3 个年度标准差变动发生的概率为 0.50%（比正态分布更厚），但其中一些每日变动被认为是不可能的。

采样周期越短，尾巴就越肥。

或者另外说：

对于较短的时间范围，1% 的概率变动将比较较长的时间范围产生更多的标准差。 （您也可以在选项表面中看到这一点）

因此，如果您以低分辨率查看回报，您就会错过这种体验。即使你看一下 2020 年的月刊，它似乎也没有你作为投资者从中感受到的感受那么重要。

加起来：

使用月度和年度决议，我夸大了风险。
但风险取决于解决方案。如果您是投资者并且可以避免查看您的账户，那么您实际上会看到波动性较小（在标准差的基础上）！这是忽略路径的论点。

远方平静，近处动荡
问题在于美国过去的回报率并不能预示未来的情况。假设 6% 的实际回报率（扣除通货膨胀因素）是激进的。
当你的投资生涯是 40 年系列中的一个时，100% 股票更多地与信念有关，而不是判断。

来自我的实际生活

放假期间我很享受的一些事情。

早上和孩子们一起做拼图。我们制作《纽约时报》系列游戏：Wordle/Letterboxed/Connections/Mini 以及Set Daily Challenge
我们一直在玩黑手党（有时称为狼人）社交推理游戏。没有什么可买的，我用一些支持 GPT 的故事讲述融入了现实生活的元素，为其增添了趣味。我把它写在这里：

四海兄弟：社交演绎派对游戏
我通过妻子的工作认识的一位朋友是一位音乐家，他的品味完全符合我的口味。他让我喜欢King Gizzard 和 The Lizard Wizard, Khruangbin ，然后他又来了——他给我发了 Natural Child 的 Be M’Guest 唱片，其中我一直在玩不停。来自所有音乐：

Natural Child 是一个三重奏，其良好而油腻的风格融合了南方摇滚、复古乡村摇滚、悠闲的 Laurel Canyon 音乐、70 年代风格的布吉音乐、一点硬摇滚，以及酒和烟枪的精心平衡。点击数

ab67616d0000b2733247b65672758c4a620d6443

做客

亲生孩子

专辑

最后，在除夕夜，我们与姻亲度过了一个寒冷的夜晚，但决定尝试一些新的东西来增添趣味……谋杀之谜晚餐。

这是我的指南：

我在新年前夜举办了一场谋杀悬疑游戏

这是我作为一个浮夸的前卫电影导演在好莱坞山举办的派对庆祝拍摄完成。和我一起的是“Patty Field”，这位服装设计师的动机显然是致命的吸引力。