通过优化 softmax 来学习 CUDA：工作日志

softmax 操作至关重要。它被广泛用作深度学习模型（如 Transformer）中的一个层，它将原始分数（logits）标准化为概率分布。此属性使其在分类任务中特别有用，其中每个输出神经元代表特定类别的可能性。优化 softmax，特别是在使用 CUDA 进行 GPU 编程的背景下，提供了许多学习机会。

在本工作日志中，我们将从对 PyTorch 的 softmax 操作进行基准测试开始，最后我们将在 CUDA 中对其进行迭代优化。用于此工作日志的 NVIDIA GPU 是一个RTX 1050Ti （这是我现在拥有的全部）。

完整的代码可以在我的 GitHub 上找到： Optimizing softmax in CUDA

让我们开始吧。

数学

在深入讨论之前，让我们花点时间了解一下 softmax 运算背后的数学原理。 Softmax 对于具有 $N$ 个元素的输入向量 $\textbf{X}$，生成具有 $N$ 个元素的输出向量 $\textbf{O}$，其中输出向量中的 $i^{th}$ 元素是定义为：

$$ \textbf{O} i = \frac{e^{x_i}}{\Sigma {k = 0}^{N}{e^{x_k}}} $$

请注意，softmax 运算取决于当前元素 $x_i$ 以及输入向量 $X$ 的所有元素的指数之和。今后我们将把这个总和称为“标准化因子”（或范数）。

通常，我们处理的不是单个向量，而是由 $M$ 行组成的 $(M, N)$ 形状的矩阵，其中每行都是由 $N$ 元素组成的向量。然后沿着该矩阵的列执行 Softmax。这里的输出将是另一个相同形状的矩阵。

在整个工作日志中，我们将使用形状为 $(1024, 32768)$ 的矩阵，即总共 $33,554,432$ 浮点数。

包含 $5$ 元素的向量上的 softmax 输出示例：

 import torch import torch.nn.functional as F vector = torch.randn(5, dtype=torch.float32) print("Input vector:", vector) # softmax along the last dimension output = F.softmax(vector, dim=-1) print("Output vector:", output)

 Input vector: tensor([-1.3701, 0.7485, 0.1610, -2.0154, 1.0918]) Output vector: tensor([0.0382, 0.3176, 0.1765, 0.0200, 0.4477])

但有一个问题：

如果 $x_i$ 的值非常大（或非常小），那么考虑到现代计算机上浮点数的精度限制，指数可能会导致上溢或下溢。我们无法代表和处理非常大或非常小的数字。这意味着对于极值，上述版本的 softmax 在数值上不稳定。

但是……有一个解决办法！我们可以修改上面的方程，使整个运算在数值上稳定且正确：在计算指数之前，我们从每个 $x_i$ 中减去向量的最大值 $x_{max}$（常数）。此减法运算将数字“移位”到可以很好地处理浮点数的范围。数值稳定的 softmax 方程变为：

$$ \textbf{O} i = \frac{e^{(x_i – x {max})}}{\Sigma_{k = 0}^{N}{e^{(x_k – x_{max})} }} $$

这个“移位”方程如何产生正确的 softmax 输出留给读者作为练习:)

PyTorch 有多快？

我们可以得到一个基线指标，了解 PyTorch 在随机初始化的矩阵上沿着最后一个维度计算 softmax 运算的速度。

按照上面的例子，我们可以快速测量softmax函数的执行时间：

 import time import torch import torch.nn.functional as F # Initialize the matrix on devuce matrix = torch.randn(1024, 32768, device='cuda', dtype=torch.float32) # Warm up _ = torch.nn.functional.softmax(matrix, dim=-1) # Ensure all CUDA operations are finished torch.cuda.synchronize() total_time = 0 n_iters = 5 for i in range(n_iters): # Measure time torch.cuda.synchronize() # Ensure all CUDA operations are finished start = time.time() _ = torch.nn.functional.softmax(matrix, dim=-1) torch.cuda.synchronize() # Synchronize again end = time.time() total_time += (end - start) * 1000 print(total_time) print(f"Softmax computation time (average): {(total_time/n_iters):.3f} ms")

 Softmax computation time (average): 7.226 ms

根据我们的快速测试，PyTorch 需要大约 7.2 毫秒来处理和计算整个矩阵的 softmax。现在，让我们看看在 CUDA 中实现 softmax 能走多远。

内核 1 – Naive softmax

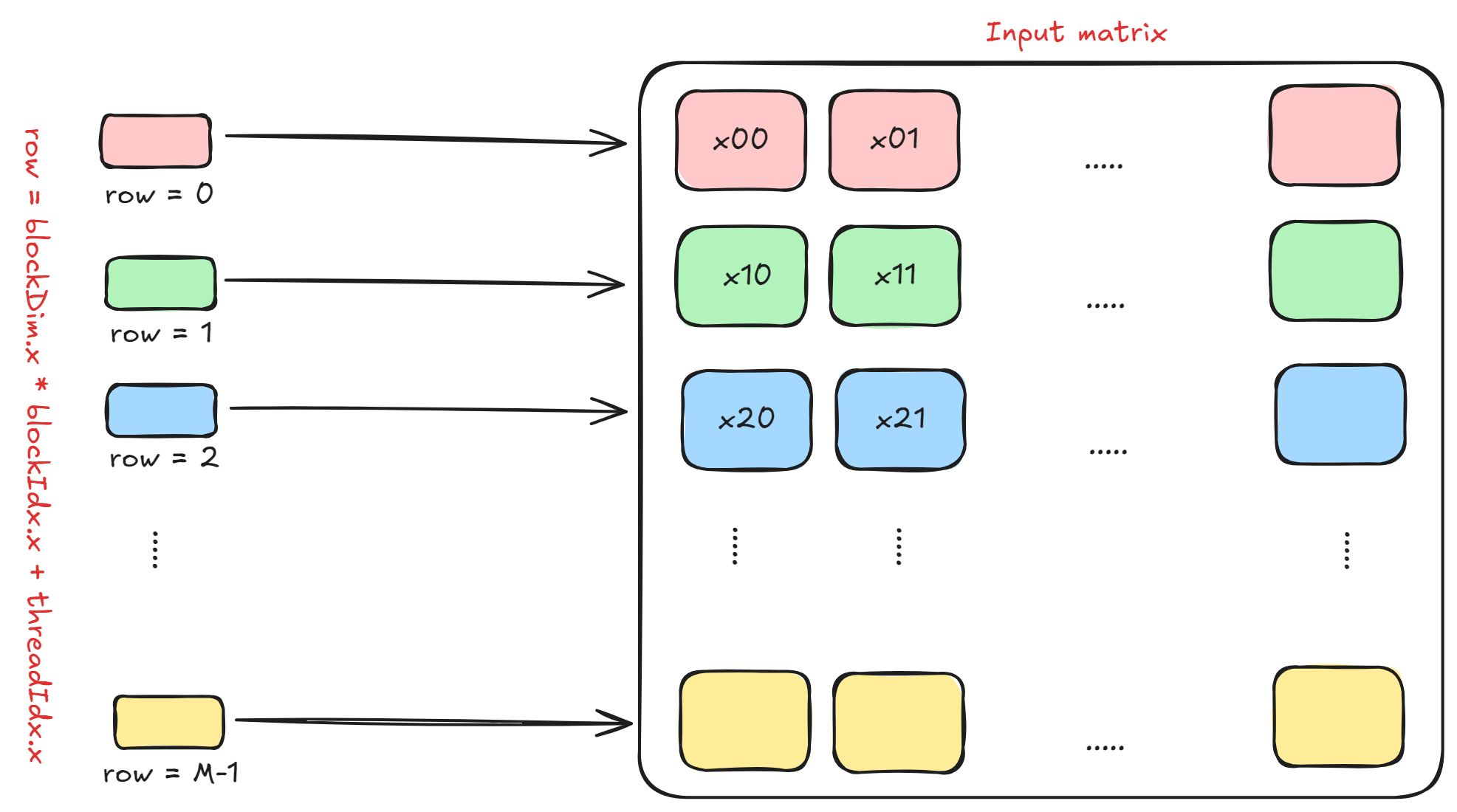
在此内核中，我们假设块中的每个线程处理并计算输入矩阵的一整行。如果一个块中的线程数量为N_THREADS ，那么我们总共需要ceil(M / N_THREADS)个块来处理整个矩阵。

下图显示了这一点。请注意， row = blockDim.x * blockIdx.x + threadIdx.x是某个块中的每个线程将处理的行。

朴素线程映射

这里的实际计算是非常直观的。 Softmax 通过输入数组进行三遍计算：

第 1 遍 – 计算最大值：首先从左（索引 = 0）到右（索引 = N – 1）遍历整个输入行以找到最大值 $x_{max}$。
第 2 遍 – 计算范数：再次从左到右遍历整个输入行，但这次使用第一遍中每个元素的 $x_{max}$ 值计算归一化因子。
第 3 遍 – Softmax 计算：再次从左到右遍历整个输入行，对于每个元素，$(x – x_{max})$ 的指数除以第二遍中计算的范数。

下面是执行此操作的具体代码片段：

 int row = blockDim.x * blockIdx.x + threadIdx.x; if (row < M) { // maximum of this row float x_max = -INFINITY; // norm factor of this row float norm = 0.0f; // output in 3 passes for (int col = 0; col < N; col++) { int i = row * N + col; x_max = max(x_max, input[i]); } for (int col = 0; col < N; col++) { int i = row * N + col; norm += expf(input[i] - x_max); } for (int col = 0; col < N; col++) { int i = row * N + col; output[i] = expf(input[i] - x_max) / norm; } }

运行该内核会产生：

 >> GPU allocation time: 10.727424 ms >> Host to device transfer time: 26.176161 ms >> Kernel execution time: 124.102112 ms >> Device to host transfer time: 37.320896 ms

朴素内核的执行时间约为 124.10$ 毫秒。与 PyTorch 的 7.2 毫秒相比，慢了 17.24 美元。

我们可以改进它吗？我们当然可以。

内核 2 – 在线 softmax

计算 softmax 的三遍根本不是最佳的。也许有一种方法可以将第一遍（计算最大值）和第二遍（计算范数）“融合”在一起。

为此，我们将利用指数的乘法性质，即

$$ e^a \cdot e^b = e^{a + b} $$

为了仅一次计算 $x_{max}$ 和范数，在每一步我们需要将“当前范数”乘以“校正项”。

例如，考虑以下输入向量：$V = [3, 2, 5, 1]$，我们需要计算其最大值和范数。现在，我们将迭代这个输入向量，看看我们需要什么校正项以及何时需要它。

假设变量 $max_i$ 和 $norm_i$ 将表示 $i^{th}$ 元素之前的最大值和范数。

从 $i = 0$ 开始：

我们有 $x_0 = 3$
当前元素明显大于$max_0$，所以$max_0 = 3$
$norm_0 = e^{(x_0 – max_0)} = e^{(3 – 3)} = 1$

请注意，在第一次迭代之后，最大值和范数的值是正确的值（但直到第一个索引）。

接下来在 $i = 1$ 处：

我们有 $x_1 = 2$
当前元素小于先前的最大值 $max_0$，因此 $max_1 = 3$ 是第二次迭代后的最大值
$norm_1 =norm_0 + e^{(x_1 – max_1)} = e^{(3 – 3)} + e^{(2 – 3)}$

我们在每次迭代时将“先前范数”值添加到“当前范数”值。

现在$i = 2$：

我们有 $x_2 = 5$
当前元素大于先前的最大值 $max_1$，因此 $max_2 = 5$ 是第三次迭代后的最大值。
我们现在看到“全局”最大值已发生变化，导致之前的规范值不正确。
如果我们将 $e^{(max_1 – max_2)}$ 乘以之前的范数来纠正它会怎么样？让我们来看看。
因此，我们得到 $ Corrected =norm_1 \cdot e^{(max_1 – max_2)} = \lparen e^{(3 – 3)} + e^{(2 – 3)}\rparen * e^{(3 – 5)} = e^{(3 – 5)} + e^{(2 – 5)}$
然后，我们只需添加当前元素的贡献： $norm_2 = Corrected + e^{(5 – 5)}$
这是正确的全球规范！我们只是使用指数乘法的性质来纠正它，然后加上当前元素的贡献。

最后在 $i = 3$ 处：

我们有 $x_3 = 1$
当前元素小于之前的最大值 $max_2$，因此全局最大值保持不变，即 $max_3 = max_2 = 5$
因此，$norm_3 =norm_2 + e^{(x_3 – max_3)} =norm_2 + e^{(1 – 5)}$

最终迭代之后，我们仍然：

$$ x_{最大值} = max_3 = 5 $$

和，

$$范数=norm_3 = e^{(3 – 5)} + e^{(2 – 5)} + e^{(5 – 5)} + e^{(1 – 5)} $$

我们只是通过使用校正项并利用指数乘法的性质，仅在一次传递中计算了最大因子和范数因子！修正项为：

$$项 = e^{(max_{i-1} – max_i)} $$

现在，要将此算法编写为 CUDA 内核，我们只需使用朴素内核并将前两个循环“融合”为一个：

 int row = blockDim.x * blockIdx.x + threadIdx.x; if (row < M) { float x_max = -INFINITY; float norm = 0.0f; // pass 1 for (int col = 0; col < N; col++) { int i = row * N + col; float curr = input[i]; if (curr > x_max) { // correct the global norm here norm = norm * expf(x_max - curr); x_max = curr; } norm += expf(curr - x_max); } // pass 2 for (int col = 0; col < N; col++) { int i = row * N + col; input[i] = expf(input[i] - x_max) / norm; } }

运行该内核会产生：

 >> GPU allocation time: 10.431488 ms >> Host to device transfer time: 25.897375 ms >> Kernel execution time: 88.149567 ms >> Device to host transfer time: 33.533314 ms

使用这个简单的技巧（也称为在线 softmax ），我们发现该内核比原始内核快 1.39$ 倍（大约 28.12$%）。

这是一个聪明的改进，但我们可以做得更多。我们需要更深入地研究如何使用一个块内的线程通过相互协作来进一步并行计算。

内核 3 – 共享内存和减少

您对 CUDA 的 GPU 编程了解得越多，您就越会意识到内存是分层结构的。下面的列表显示了不同内存层次结构的访问速度（从最快到最慢）。

寄存器（范围是每个线程）
共享内存/L1 缓存（范围是每个块）
二级缓存
全局内存（也称为 VRAM）

上面的内核仅使用全局 GPU 内存。读取和写入全局内存既昂贵又耗时，因此我们需要以某种方式减少访问和存储时间。

这里的想法是让每个块（线程块）处理输入矩阵的一行，并且每个块内的线程将仅处理整行的一部分。查看下图以了解每个线程将加载哪些元素。

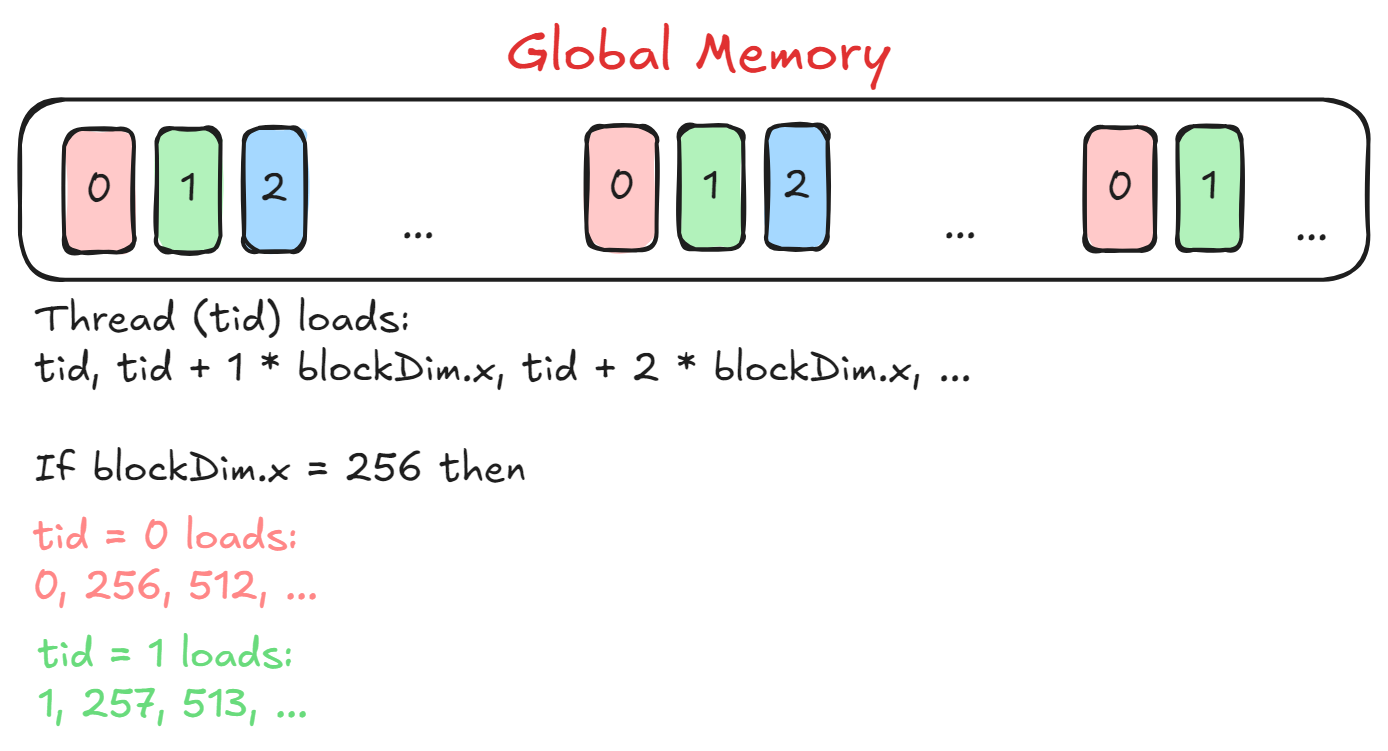
线程块加载

这里tid = threadIdx.x加载由blockDim.x间隔的元素，以便具有不同tid线程从输入行加载连续的元素。这有助于实现内存合并，其中从全局内存访问连续地址比访问随机地址更快。

但存在一个问题：要计算最大值和范数的值，我们需要访问输入行的所有元素。如果不同的线程只能访问输入行的一部分，我们将如何做到这一点？

这就是削减发挥作用的地方。请耐心听我讲这一点。

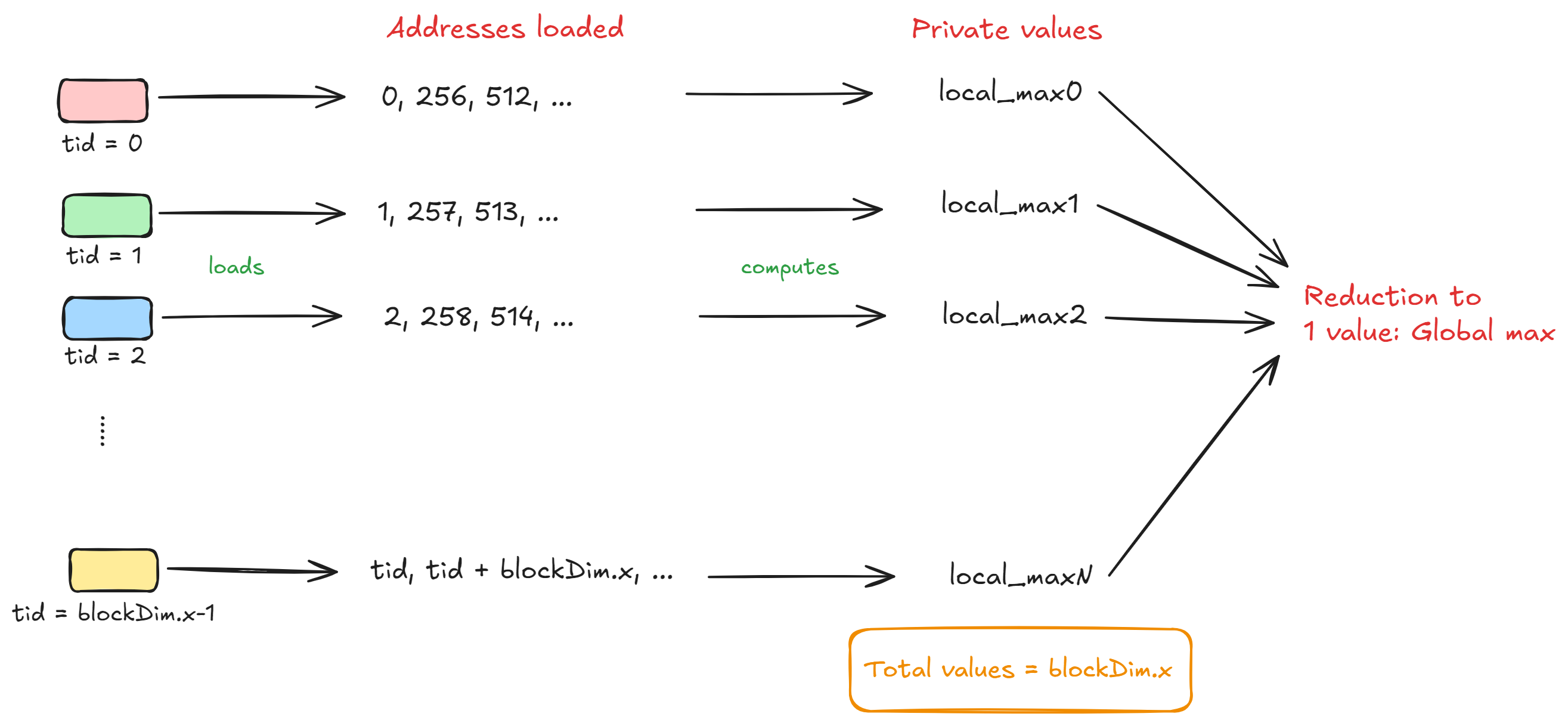
我们假设每个线程都有自己的私有变量集，称为local_max和local_norm ，并且还假设总共有N_THREADS线程。现在， tid = i的线程将使用元素i, i + blockDim.x, i + 2*blockDim.x等计算局部最大值和局部范数。

当块中的所有线程完成处理各自的块后，我们将为local_max和local_norm留下N_THREADS值。为了计算全局最大值，我们需要将这N_THREADS个局部最大值“减少”到 $1$ 全局最大值。下图将帮助您理解这一点。

最大减少量

然而，为了执行这种“块级”缩减，我们需要将局部最大值存储在块的共享内存中。每个线程将其局部最大值存储为：

 smem[tid] = local_max; __syncthreads();

请注意，我们还添加了同步屏障，以确保每个线程正确地将其局部最大值存储到共享内存中的相应地址中，并在继续减少步骤之前等待其他线程。

现在，我们将使用共享内存将N_THREADS局部最大值减少到 $1$ 值，然后将其存储在共享内存中的第一个地址 ( smem[0] ) 中。减少步骤如下所示：

 for (int stride = blockDim.x / 2; stride > 0; stride /= 2) { if (tid < stride) { smem[tid] = max(smem[tid], smem[tid + stride]); } // sync before next iteration __syncthreads(); } float global_max = smem[0]; __syncthreads();

此代码块执行O(log(N))时间复杂度的降低，这比线性降低（即O(N)复杂度）要快。让我们看一个使用 $8$ 线程进行减少的示例，其中共享内存在开始时将包含 $8$ 最大值：

最初：

 smem = [3, 7, 2, 8, 6, 4, 5, 1]

第一次迭代（步长 = $4$）：

tid < 4的每个线程将smem[tid]与smem[tid + stride]进行比较，并用最大值更新smem[tid] 。

比较：

 tid = 0: smem[0] = max(smem[0], smem[4]) = max(3, 6) = 6 tid = 1: smem[1] = max(smem[1], smem[5]) = max(7, 4) = 7 tid = 2: smem[2] = max(smem[2], smem[6]) = max(2, 5) = 5 tid = 3: smem[3] = max(smem[3], smem[7]) = max(8, 1) = 8

更新了sme：

 smem = [6, 7, 5, 8, 6, 4, 5, 1]

第二次迭代（步幅 = $2$）：

tid < 2的每个线程将smem[tid]与smem[tid + stride]进行比较并更新smem[tid] 。

比较：

 tid = 0: smem[0] = max(smem[0], smem[2]) = max(6, 5) = 6 tid = 1: smem[1] = max(smem[1], smem[3]) = max(7, 8) = 8

更新了sme：

 smem = [6, 8, 5, 8, 6, 4, 5, 1]

第三次迭代（步长 = $1$）：

tid < 1的每个线程将smem[tid]与smem[tid + stride]进行比较并更新smem[tid] 。

比较：

 tid = 0: smem[0] = max(smem[0], smem[1]) = max(6, 8) = 8

更新了sme：

 smem = [8, 8, 5, 8, 6, 4, 5, 1]

最终状态：

减少后，最大值存储在smem[0]中，即：

 global_max = smem[0] = 8

这显示了我们如何在仅 $3$ 迭代中执行缩减并从 $8$ 线程访问全局最大值。我们对local_norm进行同样的缩减，以找到全局范数值。局部范数的唯一区别是，我们不执行max操作，而是执行+操作。

以下是内核减少最大值的样子：

 __shared__ float smem[1024]; int row = blockIdx.x; int tid = threadIdx.x; // edge condition (we don't process further) if (row >= M) return; float* input_row = xd + row * N; float* output_row = resd + row * N; float local_max = -INFINITY; float local_norm = 0.0f; for (int i = tid; i < N; i += blockDim.x) { float x = input_row[i]; if (x > local_max) { local_norm *= expf(local_max - x); local_max = x; } local_norm += expf(x - local_max); } __syncthreads(); smem[tid] = local_max; __syncthreads(); for (int stride = blockDim.x / 2; stride > 0; stride /= 2) { if (tid < stride) { smem[tid] = max(smem[tid], smem[tid + stride]); } __syncthreads(); } float global_max = smem[0]; __syncthreads();

该内核的输出如下所示：

 >> GPU allocation time: 10.464928 ms >> Host to device transfer time: 22.674080 ms >> Kernel execution time: 6.612160 ms >> Device to host transfer time: 41.318016 ms

我们立即看到这个使用共享内存和缩减的内核已经比 PyTorch 的实现快了约 8.33%（1.09 倍） 。

我们可以进一步改进吗？让我们来看看。

内核 4 – 随机播放指令

该内核与前一个内核非常相似，但有一点不同。如果您仔细观察，在局部最大值和局部规范值的归约操作中，我们将访问共享内存并在每次迭代中同步线程。尽管访问共享内存很快，但如果我们可以消除共享内存和同步屏障的使用，同时减少值呢？

在解释如何操作之前，我们需要了解线程块内扭曲的概念：

扭曲是线程块内的基本执行单元。 warp 是线程块中的一组 $32$ 线程，它们同时执行相同的指令（SIMD：单指令，多数据）。 warp 中的所有线程都以锁步方式执行指令，这意味着所有 $32$ 线程同时对不同的数据执行相同的指令。如果线程块包含 $N$ 线程，则扭曲数为ceil(N / 32) 。此外，当线程束中的线程遵循不同的执行路径时（例如，由于条件语句），它会导致线程束发散，从而降低性能，因为线程顺序执行而不是并行执行。

在我们的例子中，如果blockDim.x = 1024 ，则每个块由 $32$ warp 组成（每个 warp 由 $32$ 线程组成）。

为了限制共享内存的使用，CUDA 为我们提供了shuffle 指令，这些指令是专门的内在函数，允许 warp 中的线程直接交换数据，而无需共享内存的开销。这些是扭曲级原语并且非常高效，因为它们使用寄存器来交换数据，这比使用共享内存更快（根据层次结构）。

假设在一个块中我们总共有N_THREADS个线程。这意味着，我们有NW = ceil(N_THREADS / warp_size) warp，其中warp_size通常是 $32$ 线程。现在，我们不使用共享内存进行块级缩减，而是首先执行扭曲级缩减：

从N_THREADS值中，对每个可用的扭曲进行扭曲级别的减少将使我们在整个块中留下需要进一步减少的 $NW$ 值。因此，第一个可用的扭曲可以加载剩余扭曲中的值，然后再次执行扭曲级别缩减以获得最终值。让我们考虑一个例子来缓解您的心情：

假设有 $16$ 线程已经计算出各自的局部最大值。另外，假设warp_size = 4 ，这意味着总共有 $4$ 扭曲。值为[3, 7, 2, 9, 4, 1, 8, 5, 10, 6, 12, 11, 13, 14, 15, 16] 。

第 1 步：减少扭曲程度

扭曲大小为 $4$，因此块中有 $4$ 扭曲（$16$ 线程/每个扭曲 $4$ 线程）。每个扭曲都会执行自己的缩减。

扭曲 0（线程 0 到 3：值 [3, 7, 2, 9]） ：

偏移量 = $2$:

线程 0 将其值 (3) 与线程 2 的值 (2) 进行比较：max(3, 2) = 3。
线程 1 将其值 (7) 与线程 3 的值 (9) 进行比较：max(7, 9) = 9。

偏移量 = $1$：

线程 0 将其新值 (3) 与线程 1 的值 (9) 进行比较：max(3, 9) = 9。

Warp 0 的结果：9（存储在 warp 的线程 0 中）。

扭曲 1（线程 4 至 7：值 [4, 1, 8, 5]） ：

偏移量 = $2$:

线程 4 将其值 (4) 与线程 6 的值 (8) 进行比较：max(4, 8) = 8。
线程 5 将其值 (1) 与线程 7 的值 (5) 进行比较：max(1, 5) = 5。

偏移量 = $1$：

线程 4 将其新值 (8) 与线程 5 的值 (5) 进行比较：max(8, 5) = 8。

经纱 1 的结果：8（存储在经纱的线程 4 中）。

扭曲 2（线程 8 至 11：值 [10, 6, 12, 11]） ：

偏移量 = $2$：

线程 8 将其值 (10) 与线程 10 的值 (12) 进行比较：max(10, 12) = 12。
线程 9 将其值 (6) 与线程 11 的值 (11) 进行比较：max(6, 11) = 11。

偏移量 = $1$：

线程 8 将其新值 (12) 与线程 9 的值 (11) 进行比较：max(12, 11) = 12。

Warp 2 的结果：12（存储在 warp 的线程 8 中）。

扭曲 3（线程 12 到 15：值 [13, 14, 15, 16]） ：

偏移量 = $2$:

线程 12 将其值 (13) 与线程 14 的值 (15) 进行比较：max(13, 15) = 15。
线程 13 将其值 (14) 与线程 15 的值 (16) 进行比较：max(14, 16) = 16。

偏移量 = $1$：

线程 12 将其新值 (15) 与线程 13 的值 (16) 进行比较：max(15, 16) = 16。

Warp 3 的结果：16（存储在 warp 的线程 12 中）。

步骤 2 – 块级缩减

此时，每个经纱的最大值存储在每个经纱的第一个线程中： [9, 8, 12, 16] 。

块级缩减开始。

将变形结果存储在共享内存中：

每个 warp 领导者（线程 0、4、8、12）将其结果写入共享内存 (smem)。
smem = [9, 8, 12, 16] 。

同步线程：

使用 __syncthreads() 同步线程以确保共享内存值对所有线程都可见。

使用第一变形执行最终缩减：

只有第一个 warp（线程 0-3）参与减少 smem 中的值。

第一扭曲减少 (smem = [9, 8, 12, 16]) :

偏移量 = $2$:

线程 0 将smem[0] (9) 与smem[2] (12) 进行比较：max(9, 12) = 12。
线程 1 将smem[1] (8) 与smem[3] (16) 进行比较：max(8, 16) = 16。

偏移量 = $1$：

线程 0 将 smem[0] (12) 与 smem[1] (16) 进行比较：max(12, 16) = 16。

全局块最大值：16 （存储在smem[0]中）。

此时，我们使用扭曲级别缩减获得了整个块的全局最大值。

那么如何实际执行这些扭曲级别的减少呢？ CUDA 为此提供了随机指令。我们将使用__shfl_down_sync指令来执行归约。它的工作原理如下：

它是一个 CUDA 扭曲级原语，可在扭曲内向下移动数据值。 warp 中的线程根据指定的offset交换数据，并且将从越界线程接收数据的线程分配一个默认值。 __shfl_down_sync的语法是：

 T __shfl_down_sync(unsigned mask, T var, int delta, int width=warpSize);

这里：

mask ：指定扭曲中哪些线程对此操作处于活动状态的位掩码。我们使用0xFFFFFFFF来包含 warp 中的所有线程。
var ：要移动的当前线程的值。
delta ：将值向下移动的线程数。
width (optional) ：参与操作的线程数量（必须是2的幂，最多32）。默认为扭曲大小 (32)。

考虑下面的代码：

 int val = threadIdx.x; int shifted_val = __shfl_down_sync(0xFFFFFFFF, val, 1);

对于delta = 1 ：

线程 0 获取线程 1 的值。
线程 1 获取线程 2 的值。
…
该范围中的最后一个线程获得未定义的值。

该内核的缩减代码如下所示：

 float val = local_max; for (int offset = warp_size / 2; offset > 0; offset /= 2) { val = fmaxf(val, __shfl_down_sync(0xffffffff, val, offset)); } if (blockDim.x > warp_size) { if (tid % warp_size == 0) { // which warp are we at? // store the value in its first thread index smem[tid / warp_size] = val; } __syncthreads(); if (tid < warp_size) { val = (tid < CEIL_DIV(blockDim.x, warp_size)) ? smem[tid] : -INFINITY; for (int offset = warp_size / 2; offset > 0; offset /= 2) { val = fmaxf(val, __shfl_down_sync(0xffffffff, val, offset)); } if (tid == 0) smem[0] = val; } } else { if (tid == 0) smem[0] = val; } __syncthreads(); float global_max = smem[0]; __syncthreads();

内核输出：

 >> GPU allocation time: 10.542080 ms >> Host to device transfer time: 25.580065 ms >> Kernel execution time: 5.174400 ms >> Device to host transfer time: 45.923008 ms

该内核比共享内存内核快约 1.29$ 倍（或 22.73$%）！使用 shuffle 指令也消除了在每次迭代中使用同步屏障__syncthreads的需要。

结论

在此工作日志中，我们从 PyTorch 开始迭代优化 softmax 操作，然后为其编写自定义 CUDA 内核。通过上述改进，我们的自定义 softmax CUDA 内核比 RTX 1050Ti 上的 PyTorch 快约 1.41 美元倍（或 29.17 美元%）。

完整的代码可以在我的 GitHub 上找到： Optimizing softmax in CUDA
在 X（以前称为 Twitter）上关注我，了解有关 ML、CUDA 和我的生活的实时更新： Twitter 个人资料

感谢您的阅读！

原文： https://maharshi.bearblog.dev/optimizing-softmax-cuda/