想象一下,您的目标是在一小部分人口被感染时感染一种新疾病。然而,您可能用来检测异常情况的许多迹象,例如看医生或排入废水中,将取决于当前感染的人数。这些有何关系?
底线:如果我们将考虑范围限制在任何人注意到异常情况之前的时间,此时人们没有改变自己的行为来避免这种疾病,那么绝大多数人仍然容易受到影响,并且传播可能呈指数级增长,那么:
发病率=累计感染ln(2)倍增时间
我们来推导一下这个吧!我们将“累积感染”称为 c(t),将“倍增时间”称为 Td。所以这是时间 t 的累积感染:
c(t) = 2 t Td
使用自然指数,数学会更容易,所以让我们定义 k = ln (2) Td 并切换我们的底数:
埃克特
我们将“发生率”称为 i(t),它将是 c(t) 的导数:
i(t) = d dt c(t) = d dt e kt = ke kt
所以:
i(t) c(t) = ke kt e kt = k = ln (2) Td
这意味着: i(t) = c(t) ln (2) Td
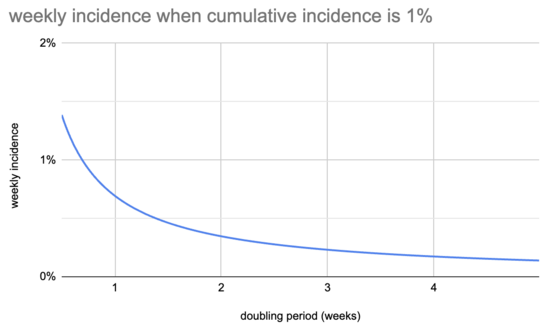
这看起来像什么?下面是累计发病率达到1%时每周发病率的图表:
例如,如果每周翻倍,那么当 1% 的人曾经被感染时,0.69% 的人在过去 7 天内被感染,相当于曾经被感染的人的 69%。如果每三周翻一番,那么当 1% 的人曾经被感染时,本周就有 0.23% 的人被感染,即累积感染率的 23%。
但这真的正确吗?让我们通过一些非常简单的模拟来检查我们的工作:
def 模拟(doubling_period_weeks):
累积感染阈值 = 0.01
初始每周发生率 = 0.000000001
累积感染数 = 0
当前每周发生率 = 0
周 = 0
而累积感染 < \
累积感染阈值:
周 += 1
当前每周发生率 = \
初始每周发生率 * 2**(
天/doubling_period_weeks)
累积感染数 += \
当前每周发病率
返回当前_每周_发生率
对于范围 (50, 500) 内的 f:
加倍_周期_周 = f / 100
打印(加倍_周期_周,
模拟(doubling_period_weeks))
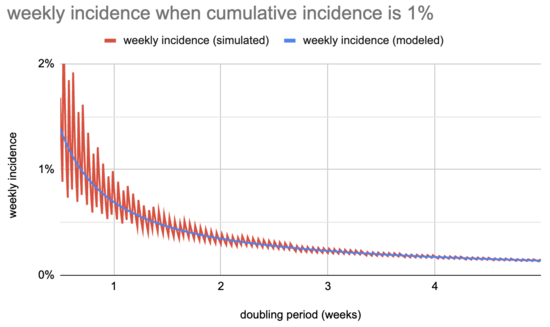
这看起来像:
模拟线是锯齿状的,特别是对于短的倍增周期而言,但这并不是特别有意义:它来自于一次运行一周的计算以及某些周将略高于或略低于(任意)1% 目标。
原文: https://www.jefftk.com/p/weekly-incidence-vs-cumulative-infections