正多边形有多少种三角剖分方法？

在这篇文章中，我们想要计算通过用不相交的直线连接顶点来将正多边形 [1] 划分为三角形的方法数量。

正方形

对于正方形，有两种可能性：我们要么连接西北角，要么连接东南角，

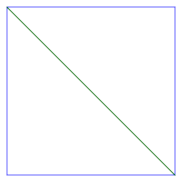
聚三1.png

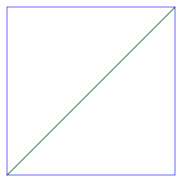
或者我们连接西南角和东北角。

聚三2.png

五角大楼

对于五边形，我们选择一个顶点并将其连接到两个不相邻的顶点。

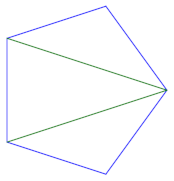
聚三3.png

我们可以对任何顶点执行此操作，因此有五种可能的三角剖分。所有五个三角剖分都是同一三角剖分的旋转。如果我们认为这些旋转是等价的怎么办？我们稍后会讨论这个问题。

六边形

对于六边形来说，事情就更有趣了。我们可以再次选择任何顶点并将其连接到所有不相邻的顶点，从而给出六个三角剖分。

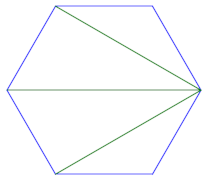
聚三4.png

但还有更多的可能性。我们可以连接所有其他顶点，在内部创建一个等边三角形。我们可以通过两种方式来完成此操作，连接偶数编号的顶点或奇数编号的顶点。任何一个三角测量都是另一个三角测量的旋转。

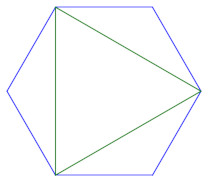
聚三五.png

我们还可以以锯齿形图案连接顶点，在内部创建 N 形图案。我们还可以将该三角测量旋转一圈或两圈。（三圈又给了我们同样的模式。）

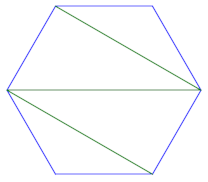
聚三六.png

最后，我们还可以连接顶点，创建向后 N 模式。

聚三七.png

一般情况

回顾一下，我们有 2 种对正方形进行三角剖分的方法，5 种对五边形进行三角剖分的方法，以及 6 + 2 + 3 + 3 = 14 种对六边形进行三角剖分的方法。另外，对三角形进行三角剖分只有一种方法：什么都不做。

令C _n为对正则 ( n + 2) 边形进行三角剖分的方法数。那么我们有C ₁ = 1、 C ₂ = 2、 C ₃ = 5 和C ₄ = 14。

一般来说，

$C_n = \frac{1}{n+1}\binom{2n}{n}$

这是第 n 个加泰罗尼亚数字。

加泰罗尼亚数字是许多问题的答案。例如， C _n也是对n + 1 项的乘积完全加括号的方式数，以及具有n + 1 个节点的满二叉树的数量。

加泰罗尼亚数已经得到了很好的研究，我们知道渐近

$C \sim \frac{4^n}{n^{3/2} \sqrt{\pi}}$

所以我们可以估计大n的C _n 。例如，我们可以使用上面的公式来估计对 100 边形进行三角剖分的方法数量为 5.84 ×10 ⁵⁵ 。第 98 个加泰罗尼亚数更接近 5.77 ×10 ⁵⁵ 。两个要点：加泰罗尼亚数字增长非常快，我们可以使用渐近公式在一个数量级内估计它们。

同等等级

现在让我们返回并再次计算三角剖分的数量，将三角剖分的某些变体视为相同的三角剖分。

我们将考虑同一三角测量的旋转仅计算一次。因此，例如，我们会说只有一个五边形的三角剖分和四个六边形的三角剖分。如果我们把镜像看成同一个三角剖分，那么一个六边形就有3个三角剖分，算上N个图案和后面的N个图案是一样的。

分组轮换

将旋转分组在一起的n边形三角剖分的等价类的数量是 OEIS 序列A001683 。请注意，序列从 2 开始。

OEIS 给出了该序列的公式：

$a(n) = \frac{1}{2n}C_{n-2} + \frac{1}{4}C_{n/2-1} + \frac{1}{2} C_{\lceil (n+1)/2\rceil - 2} + \frac{1}{3} C_{n/3 - 1}$
其中，当x不是整数时， C _x为零。所以a (6) = 4，正如预期的那样。

对旋转和反射进行分组

将旋转和反射分组在一起的n边形三角剖分的等价类的数量是 OEIS 序列A000207 。请注意，该序列从 3 开始。

OEIS 还给出了该序列的公式：

$a(n) = \frac{1}{2n}C_{n-2} + \frac{1}{4}C_{n/2-1} + \frac{1}{2} C_{\lceil (n+1)/2\rceil - 2} + \frac{1}{3} C_{n/3 - 1}$

如前所述，当x不是整数时， C _x为零。正如预期的那样，得到(6) = 3。

OEIS 页面上的公式有点令人困惑，因为它使用C ( n ) 来表示C _{n -2} 。

正方形

五角大楼

六边形

一般情况

同等等级

分组轮换

对旋转和反射进行分组

相关帖子