博客嘉年华是发现新博客的一种方式。特定主题(例如数学)的作家轮流主持嘉年华,以不同作家最近的帖子为特色。博客嘉年华曾经很常见,但现在大多数已经消失了。
然而,数学嘉年华是最古老的嘉年华之一,并且仍然活跃,今年是第 235 届嘉年华,这一事实证明了这一点。
我曾多次在这里举办狂欢节。第一次是#50 ,最近一次是#222 。
非周期性是嘉年华的一种元主机:您可以通过访问此站点找到过去和未来的主机。
数字琐事
按照惯例,第n届数学嘉年华会以有关数字n 的琐事开始。
根据Number Gossip 的说法,“235 是最小的数字,其前两位数字是不同的素数,因此它们的总和等于第三位数字。”
235 是一个中心三角形数。下图包含 235 个点。
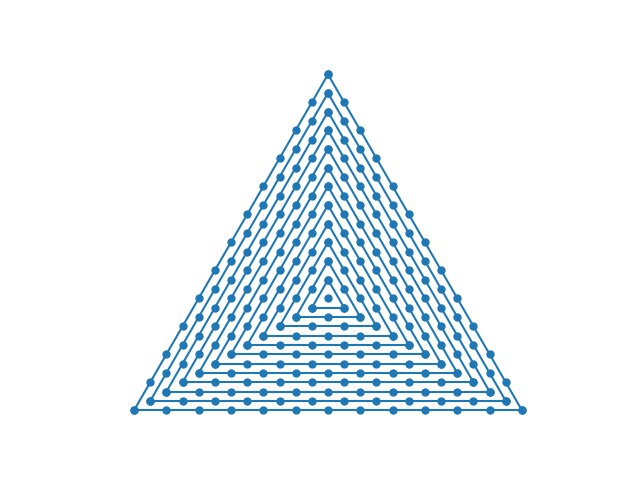
235 是半素数,即两个素数的乘积,在本例中为 5 和 47。有一个定理,如果p和q是素数, p > q且q不是 a,则只有一组pq阶p − 1 的因子,因此只有一组有 235 个元素,即 5 阶和 47 阶循环群的直和。
帖子提交
这次有两个陶哲轩网站的链接。第一个是人工智能数学基金的公告。第二篇是陶老师关于四元数和球面三角学的简短笔记。
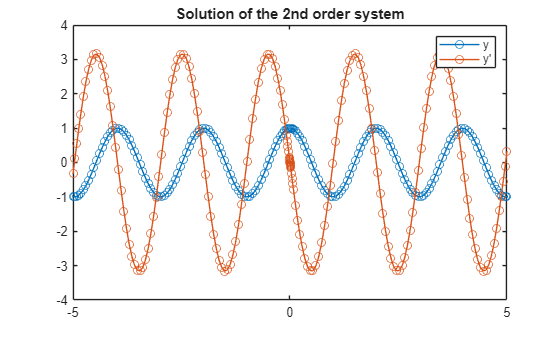
我们有一个来自Mike Croucher的关于在 MATLAB 中求解高阶 ODE的帖子的链接。与许多软件环境一样,MATLAB 不直接支持高阶 ODE,但支持一阶 ODE 系统,并且您始终可以将前者转换为后者。 Croucher 展示了如何进行这种转换,首先是手动进行,然后使用 MATLAB 的符号计算功能。
Ionna Georgiu发布了一系列有关各种主题的视频,其中包括比毕达哥拉斯早一千年的我们现在所说的毕达哥拉斯定理的证据。
有人向 Kevin Buzzard 撰写的Xena Project帖子提交了有关在精益中形式化费马大定理(FLT) 的帖子。这篇文章中启发我的一句话是“我们没有将 20 世纪 90 年代老式的 FLT 证明形式化。从那时起,许多人的工作……导致证明被概括和简化……”因此,在一代人的时间里,怀尔斯的证明已经从开创性变成了过时的。
Sophie Huiberts制作了一个名为“开放问题和饮食问题”的视频,内容涉及线性规划,优化受线性约束的线性目标函数。解决此类优化问题的单纯形法在实践中比在最坏情况理论中表现得更好。实际上,执行算法所需的时间与问题的规模成正比,但我们可以构造人工问题,使所需的时间随着问题的规模呈指数增长。惠伯特研究了单纯形法为何如此有效的概率解释,但得出的结论是该解释并不令人满意。
数学狂欢节 235后首次出现在John D. Cook上。
原文: https://www.johndcook.com/blog/2025/01/02/carnival-of-mathematics-235/