建模振荡的起伏

Fruzsina Agocs 是熨斗研究所计算数学中心的研究员。学分：约翰斯莫克

Fruzsina Agocs的职业生涯始于一名理论宇宙学家。但她很快发现，没有足够的数学和计算工具来运行她想要使用的模型。当她深入研究数学来制作她需要的工具时，Agocs 发现她喜欢这种方法。这让她走上了一条专注于为其他科学家在他们自己的模型中使用的更好工具的道路。

如今，Agocs 是Fl​​atiron Institute计算数学中心(CCM) 的研究员，她在该中心的数值分析小组工作。在此之前，她在剑桥大学获得了理论和计算宇宙学博士学位，以及物理学硕士和学士学位。

Agocs 与西蒙斯基金会谈论了她的工作和令人惊讶的楼梯声学效果。为清楚起见，对对话进行了编辑。

你现在在做什么项目？

我研究振荡系统。这些系统具有某种来回或上下的重复运动。一个非常简单的例子就是跷跷板。然而，大多数振荡系统要复杂得多。描述它们的方程式不能由人类使用纸和笔来解决。即使是计算机也很难求解这些方程式，需要很长时间才能得出近似解。

我正致力于设计和实施一些方法，使计算机更容易求解这些方程，并高效、准确地求解。其中一个项目是开发数值方法来评估宇宙学模型。在宇宙历史的早期——大爆炸后的最初时刻——物质密度出现振荡。我正在研究如何弄清楚物质是由哪种粒子构成的，以及物质如何与其他粒子和自身相互作用。我也对那个关键时刻的时空曲率很感兴趣——本质上宇宙的几何结构是什么。这种曲率很重要，因为它可以告诉我们很多关于宇宙的整体演化和最终命运的信息。

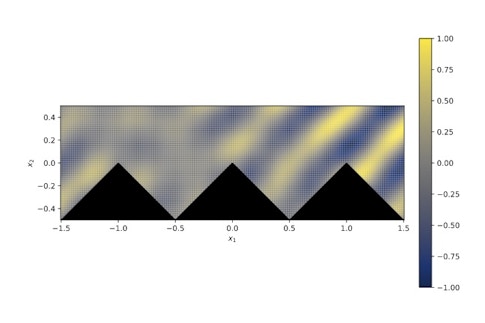从无限楼梯散射的声波的数值模拟。图片来源：Fruzsina Agocs

我最近开始了另一个基于声学的项目。我正在研究声波从称为准周期表面的特定表面的散射。这种类型的表面的一个例子是无限高的楼梯。显然，这些在现实生活中并不存在，但那里有一些很长的阶梯，例如美索不达米亚金字塔、玛雅神庙和希腊剧院等古老的阶梯式神庙。这些有很长的楼梯，表现出有趣的声学现象。例如，声音沿着楼梯向上传播得非常好，如果您在楼梯附近拍手，反射的声音听起来可能像唧唧声或雨滴声，而不是拍手声。我想以数字方式重现这些声学现象，因为有了计算机，我们终于拥有了高精度执行此操作的工具。最终，了解这些表面如何反射声音有助于指导礼堂等建筑物的设计。

为什么分析这些表面如此困难？

楼梯在数学上很有趣，因为它提出了一些独特的挑战，即两个楼梯相交的点——拐角——在数学中被描述为一个奇点。这意味着当你写下一个公式来描述这一点时，你会得到一个无穷大的值，这是计算机无法处理的。当您以数值方式解决此问题时，在接近奇点时必须非常小心，以免失去准确性。

另一个挑战来自楼梯的无限长度，因为天真地这将导致任何计算机代码的运行时间无限长。为了克服这个问题，人们必须利用结构的重复模式——它的对称性——将问题减少到楼梯的单个重复单元。有了这个数学技巧，求解无限楼梯实际上比求解真正长的有限楼梯更简单。

你如何着手模拟这些系统？

我每天都会做很多纸笔分析工作。我推导出相关方程，看看是否可以走捷径或找到可以在我的模型中使用的任何简化。我还从事算法设计，这实际上是在黑板上为我的代码制作蓝图，弄清楚我希望它如何工作以及我需要哪些参数。然后当然是实际编写代码。但我的大部分工作都在一张纸上。我编写的每一行代码都进行了大量数值分析。

你希望其他人使用你的代码吗？

是的，我强调制作可供他人使用的工具。当我完成一个项目时，我首先会以科学期刊的形式发布对我使用的方法和任何相关证明的非常详细的描述。这有助于人们了解方法和代码的限制。然后我将代码作为开源软件发布，通常发布在经过同行评审的开源软件期刊中。

我还与来自世界各地的研究人员合作开展了各种项目。例如，我与德国哥廷根大学的一组天体物理学家一起研究粒子物理问题。他们正在对可能成为暗物质候选者的不同粒子进行建模，但在模型的某些细节方面需要帮助。这些研究人员就搜索这些粒子所需的模型提供了指导，我帮助提高了运行模型所需的计算方法的准确性和速度。

最终，我的目标是让科学家能够考虑以前难以计算的模型。为此，我的方法需要健壮且开箱即用，因此我非常注重编写高质量的代码。我认为重要的是要证明您的代码确实有效，而不仅仅是一些示例来证明它在那些特定情况下有效。与 CCM 的人们合作使我能够利用其他人的专业知识来帮助严格证明该方法有效并突破高精度数值计算的界限。