阿布拉莫维茨和斯特冈有很多有趣的情节。这篇文章将重点关注下面的图,图 9.4,可在此处获取。
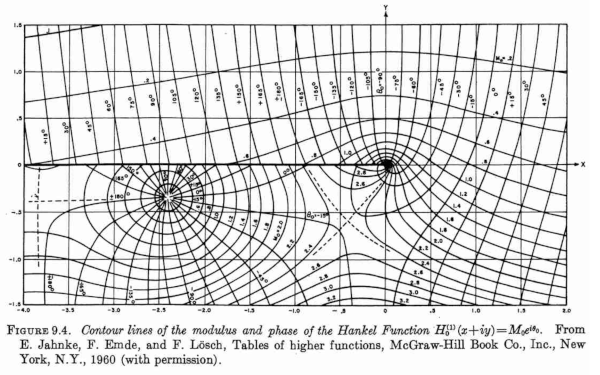
我们将解释情节是什么并大致重现它。
该图来自贝塞尔函数一章,但标题说它是汉克尔函数H 0 (1)的图。为什么是汉克尔函数图而不是贝塞尔函数图? Hankel 函数是第一类和第二类 Bessel 函数的线性组合:
H 0 (1) = J 0 + Y 0
有关 Hankel 函数及其与 Bessel 函数的关系的更多信息,请参见此处。
该图是两种等值线图的叠加:一种用于恒定幅值线,另一种用于恒定相位线。也就是说,如果函数值以r e i θ 的形式书写,则一张图显示常数r的线,另一张图显示常数 θ 的线。
我们可以使用以下 Mathematica 命令粗略地重现幅度等值线图:
ContourPlot[Abs[HankelH1[0, x + I y]], {x, -4, 2 }, {y, -1.5 , 1.5 }, 轮廓 -> 20,轮廓着色 -> 无,纵横比 -> 1/2]
这会产生以下情节。
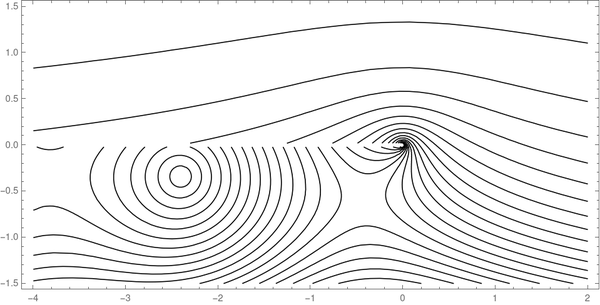
同样,我们可以在 Mathematica 命令中将Abs替换为Arg ,并将Contours增加到 30,以获得以下相位等高线图。
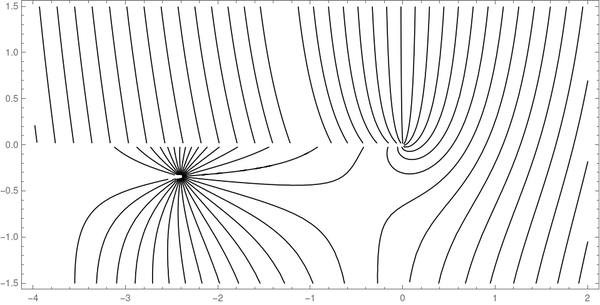
最后,我们可以使用 Mathematica 的Show命令将两个图堆叠在一起。
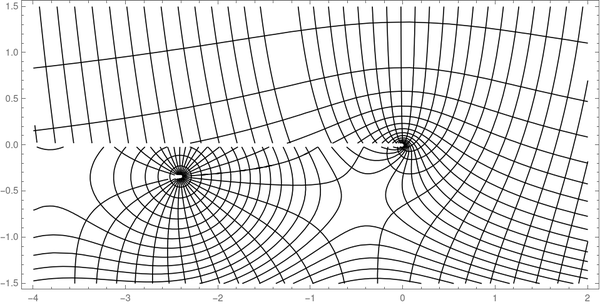
顺便说一句,你可以清楚地看到中间被切断的树枝。当您从第二象限顺时针移动到第三象限时,汉克尔函数是连续的(甚至是解析的),但由于分支切割,它在负实轴上是不连续的。
相关帖子
A&S 的复制 Hankel 情节首次出现在John D. Cook上。
原文: https://www.johndcook.com/blog/2025/01/22/duplicating-hankel-plot-from-as/