在神经活动中搜索形状

盲人与大象的寓言讲述了一群盲人第一次遇到大象的故事。每个人都感觉到动物的不同部分，并向其他人描述它。归根结底，每个人对“大象”的概念是所有个体的特殊经历的混合体。现代神经科学面临着类似的挑战。行为背后的神经活动非常复杂。在动物执行复杂任务时记录许多神经元的新技术为研究人员提供了前所未有的复杂性视图。但就像盲人摸大象一样，他们需要一种方法来理解它——破译一个躯干或一只脚的等价物，理想情况下，将这些部分拼凑成一个有凝聚力的整体。

分析神经活动结构的新方法——即其几何结构和拓扑结构——提供了一种筛选这种复杂性的方法。 “这是思考高维神经群体中神经计算和编码的下一个前沿，”熨斗研究所计算神经科学中心的项目负责人SueYeon Chung说，他写了许多关于神经反应中几何表示的论文。 “即使在传统上难以表征的大脑区域，当你观察神经活动的高维几何形状时，也会发现结构。通常，这些结构在动物或不同任务之间持续存在，揭示了共性和差异。我认为这就是它如此令人兴奋的原因。”

两篇新论文强调了这种方法的潜力，它们使用新颖的分析方法来揭示几何形式，从而深入了解电路的计算方式。他们各自的见解说明了这些方法的力量和未来的挑战，以及不同神经回路的功能能力的范围——从简单和优雅到复杂和强大。虽然这些努力让我们得以一窥大脑中一些更“复杂的大象”，但这只是一个开始。研究人员仍然需要开发新工具来分析更复杂的形式并综合出现的脱节见解。他们最终将能够构建多完整的画面仍然是一个悬而未决的问题。

简单的大象

Fiete 的分析表明，这里用颜色表示的头部方向位于一维流形——一个环上。由于歧管的弯曲形状，它似乎与自身交叉。但 Fiete 的分析揭示了它的真实本质，其形式并不取决于它的可视化程度。改编自 Chaudhuri 等人。 2019，自然神经科学。合乎逻辑的第一步是关注“简单大象”：以足够复杂的方式对信息进行编码的神经回路不是微不足道的，而是足够简单以产生可理解的洞察力。 2019 年，麻省理工学院理论神经科学家、Simons Collaboration on the Global Brian (SCGB) 的研究员Ila Fiete展示了在丘脑的头部方向细胞中编码信息的简单而优雅的方式。 Fiete 和合作者使用一种新颖的分析方法来表明头部方向网络尽可能简单地表示这个变量；该电路的神经活动状态的集合（称为流形）被限制在一维环中，使得沿环的位置对应于头部方向。

这样的发现引出了是否存在其他“简单大象”电路的问题。在《自然》杂志上发表的一项新研究中，Edvard 和 May-Britt Moser 及其合作者使用大量并行神经记录来说明长期以来备受推崇的“网格单元”系统就是这样一个电路。

Mosers 夫妇在 2005 年发现了网格细胞，这一成就使他们获得了 2014 年的诺贝尔生理学或医学奖。这些独特的细胞位于内侧内嗅皮质中，当动物在太空中航行时，它们会定期发射，形成网格状图案叠加在物理世界上时的神经活动。许多研究人员继续推测，这个大脑区域使用与这些细胞活动的重复性质唯一匹配的坐标系统来编码动物的位置。包括Fiete在内的几位研究人员的工作几乎证实了这一理论，他们使用现有数据、常规分析和数学理论的组合来描绘电路如何运作。但是，如果不同时从许多细胞中记录，直接验证他们的许多预测是不可能的。 “网格单元非常稀疏，”Fiete 说。 “如果你坚持使用传统探针，如果幸运的话，你会从少数细胞中记录下来。”但 Fiete 预测，要完全可视化网络的编码方案需要记录 40 到 60 个细胞。

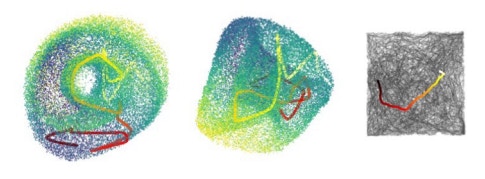Mosers 发现的两种不同的环面视图，以及动物在空间中的轨迹（右）叠加在歧管表面上。改编自 Gardner 等人。 2022，自然。

为了克服这一限制，Mosers 的团队使用 Neuropixels 探针同时记录了数百个网格单元——只有使用如此高密度的记录电极才能实现这一壮举——同时大鼠在开放空间中自由移动。他们使用了两种相关的方法来分析神经数据，这两种方法都试图对观察到的神经活动所定义的神经流形的性质做出陈述。第一类描述了神经流形的几何形状：它的一般性质以及当神经反应以图形方式绘制时形成的形状的细节。

使用标准但重要的是非线性方法将许多神经反应及时减少到一组较小的坐标，作者发现网格细胞的反应呈环面或空心甜甜圈的形状。

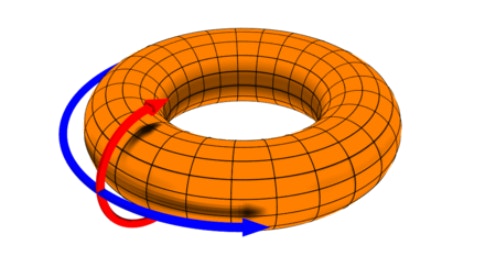环面是表示两个周期变量的最自然的坐标系。空间一维的重复网格单元活动沿环面环之一编码，而空间另一维的活动沿另一维编码。

正如环是表示周期性一维变量（如头部方向）的最简单的编码方案一样，环面是表示两个周期性变量的自然形状。在最简单的情况下，空间一维的重复网格单元活动沿环面环之一编码，而空间另一维的活动沿另一维编码。由于研究人员发现了独特的非平面几何形状，非线性方法对于获得这种洞察力至关重要。

几何分析可以提供特定的见解，在某些情况下，例如网格单元，甚至可以提供可以直观显示的见解。然而，几何分析不容易得出精确的定量陈述，也不能轻松比较来自不同实验或不同动物的多个流形。为了克服这些限制，研究人员转向了第二类分析，该分析侧重于神经流形的拓扑结构。拓扑分析的目的不是描述流形的形状，而是提供对其属性的抽象总结，例如它拥有的孔和空腔的数量和种类。

虽然几何分析提供了对具有可视化潜力的神经流形的更丰富的描述，但拓扑分析提供的更简单和更抽象的描述提供了一种紧凑的描述，虽然是零碎的，更易于比较。 “如果你想在高度可变的表示中找到共同特征，拓扑数据分析比几何方法要好得多，因为有时你想忽略在欧几里得比较中可能存在的低级细节，”Chung 说。

拓扑表征将复杂形状简化为一组数字，指示对象中不同复杂度的孔的数量。例如，一组连体环（左）有两个“一维”孔（每个环内的空间），一个球体（中心）有零个一维孔，但有一个“二维”孔（一个空腔）球体），一个圆环面有两个一维孔和一个二维孔。改编自 Chaudhuri 等人。 2019，自然神经科学。

例如，环面流形的拓扑特征将记录两个环的存在——一个在从上方观察甜甜圈时可见，另一个在您沿着甜甜圈边缘移动时可以看到，进出甜甜圈的中心——还有一个封闭的空腔，当你沿着甜甜圈中间的中心轴移动时，可以看到这个空腔。当研究人员将这种方法应用于网格单元数据时，他们发现了他们最初在视觉上识别的圆环的拓扑特征。他们能够在多个网格单元记录中定量地确认这些特征，这表明它是这个大脑回路的一个强大特征。此外，从睡眠动物记录的神经活动中存在环面特征，这表明网格细胞网络的内部连通性单独定义了其活动所在的神经流形。

这些结果证实了长期存在的假设，并提供了对这个大脑区域如何以一种保持不变的方式编码空间的见解，而不管动物位于何处以及它在做什么。尽管 Fiete 和其他人长期以来预测这些类型的记录会出现圆环，但 Mosers 的工作以惊人的细节阐明了这一理论：“以视觉方式展示它是非常强大的，”Fiete 说。

这一发现的一个特别值得注意的特征是，即使动物从事相当复杂的行为，包括在复杂环境中不受约束的导航，也会出现如此简单的几何形状。随着行为变得更加复杂，许多研究人员发现神经表征变得更加复杂，这使得 Mosers 的发现在某些方面令人惊讶并且通常非常令人满意。 “像网格单元系统这样的系统的美妙之处在于，尽管行为复杂，但它们仍然保持简单，”Fiete 说。

拼凑复杂的大象

不幸的是，网格单元环面极其简单但非平凡的几何形状可能很少见，特别是对于从事更复杂计算的神经回路，这些计算是更复杂行为的基础。普林斯顿神经科学研究所的博士后研究员曼努埃尔·肖特多夫说：“我们可以产生的所有可能的行为都存在这种有序的结构，这几乎是不可思议的。”

Schottdorf 和他的合作者Edward Nieh于 6 月在Nature上发表的研究表明，随着大脑“大象”变得更加复杂，所面临的挑战。该研究由 SCGB 研究员David Tank和Carlos Brody领导，应用了类似的高级数学分析和来自从事导航的动物的高密度神经记录的组合。他们在这种更复杂的行为中发现的神经编码图与网格细胞系统的整齐弯曲的圆环相去甚远，这暗示了他们研究的大脑区域具有更复杂的功能作用。

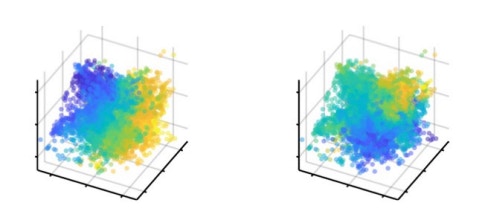海马流形的几何形状虽然是低维的，但与网格单元的环面相比，直观性要差得多。然而，沿着流形编码的任务相关变量的运动，例如位置（左）和可用于指导其决策的证据（右），其中颜色表示每种情况下每个变量的值。改编自 Nieh 等人。 2021，自然。

研究人员记录了海马体的神经反应，海马体是导航的关键大脑区域，因为动物在虚拟迷宫中导航，需要它们跟踪视觉线索。研究人员使用了一种新的分析工具，称为神经动力学的流形推理，或MIND ，来揭示由该电路活动定义的神经流形的几何结构。与网格细胞的情况一样，研究人员发现神经活动仅限于低维曲面。尽管流形没有像圆环那样自然直观的几何形状，但找到这样一个相对低维的结构是有帮助的，因为它提供了与此行为相关的变量的紧凑表示。沿流形的每个方向的运动对应于每个行为相关变量的变化，例如可用于指导其决策的位置或证据，就像沿网格单元环面的每个环的运动编码了空间中的运动方向一样。重要的是，非线性流形（只能通过 MIND 等非线性方法检测）将稳健预测流形上其他神经元的响应所需的维数减少到大约四个。主成分分析等线性方法需要超过 40 个维度。

为了解决导航任务，从技术上讲，动物只需要两个变量——它们的位置和它们对指示转向哪个方向的视觉线索的记忆。研究人员发现，这两个变量都是沿流形编码的，但其他变量也是如此，包括动物先前的选择及其头部方向。这种额外的表示复杂性表明海马体的功能与网格细胞系统完全不同。 “这是一种复杂的行为，因此鼠标可能对可能相关的变量保持开放态度，”Schottdorf 说。 “尽管流形可能代表与任务无关的变量，但代表更多可能在以后变得相关的候选变量也许没有害处。”这种灵活性和复杂性表明，海马体可能是一个关键的电路节点，可以实现更一般的行为，比如可能需要更复杂的编码方案的认知。

尽管研究人员没有研究海马流形的拓扑结构，但他们发现它似乎是大约四维的，这表明这样做会带来独特的挑战。 Fiete 说，对于高于二维的弯曲流形，识别拓扑特征的现有方法可以提供其形状的抽象表征，但与网格单元环面令人愉悦的优雅相去甚远。问题在于，高维弯曲流形的形状变得过于复杂，我们无法直观地感知——像圆环和球体这样的二维弯曲流形可以在 3 维空间中可视化，但除此之外，我们对形状的直观感觉开始动摇。 “拓扑的强大之处在于它会告诉我们关于流形的一些事情——它会给我们一系列特征，但是，就像盲人和大象一样，你仍然必须将它们拼凑在一起，”她说。网格单元网络的拓扑和几何描述提供的统一图片，令人满意地将双环单腔物体与熟悉的环面形状联系起来，进一步突出了这一发现可能是多么罕见。对于更复杂的拓扑流形，我们可能无法得到更深层次的直观图景。理论神经科学家将不得不组装流形的零碎拓扑描述，以尽可能地设想大象。

尽管理解高维流形对理论神经科学家提出了新的挑战，但这项任务并非没有希望。 “我们可以希望，如果存在比二维环面更高维的流形，也许它们可以分解成更容易表征的低维结构，”Fiete 说。 Tank 和 Brody 的工作表明，海马流形内有系统的成分，自然会导致这种类型的分解。例如，当研究人员在任务中添加一个新变量时，流形结构增加了一维。 Schottdorf 说：“这至少表明存在某种建设性机制在起作用”，逐个维度地组装流形维度。此外，Tank 实验室的相关工作引入了一个诱人的理论，即在此决策任务期间由其他大脑区域构建的流形实际上会分解，特别是分解成两个环，一个用于每个可能的决策。预计未来的流形不会那么宽容，Fiete 正致力于开发用于识别如何将复杂的流形分解为更简单部分的工具，希望它能阐明比 tori 复杂得多的流形。

一个希望是对复杂流形的进一步研究将揭示它们实际上是由多个简单对象组成的，例如一组连体环。改编自 Koay 等人。 2022 年，神经元。

在这两项研究中，神经反应仅限于流形，并且它们在没有网格单元流形的外部感觉输入的情况下持续存在的事实提供了强有力的证据，证明这些神经回路被很好地描述为连续吸引子网络。这些网络模型是理论神经科学的基石，长期以来一直是神经电路如何执行计算的主要模型，例如记忆刺激、将新刺激与以前的信息相结合，以及使用记忆或编码的刺激做出决策。但它们的发展主要集中在它们的理论特性上，只有有限的实验证据。对于位置或方向等连续变量进行编码的情况，这些模型的标志是所有网络活动最终迁移到的首选网络状态的低维空间——换句话说，是一个流形。新的分析工具，例如为研究拓扑和几何而开发的工具，最终使神经科学家能够凭经验观察神经活动中的流形，这表明连续吸引子网络不仅仅是理论家的沉思。

需要进一步的实验研究来了解这些模型如何完全捕捉真实神经活动的特性。例如，其他神经活动流形是否具有吸引子动力学的特征，如果是，它们是否与理论吸引子模型对应物一样对噪声具有鲁棒性，仍然是一个悬而未决的问题。 “了解这些连续吸引子是如何通过发展组装的，以及它们是否可以通过学习形成是一个令人兴奋的前沿领域，”Fiete 说。